
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是
【答案】
(1)(1,1);(1,3);(1,4);(2,1);(2,2);(2,3);(2,4);(3,1);(3,2);(3,3);(3,4);(4,1);(4,2);(4,3);(4,4)
(2)0.25;0.25;0.25
【解析】解:(1)填表如下:
b | 1 | 2 | 3 | 4 |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
从图表可知,共有16种等可能的情况,其中两次着地的面点数相同的情况有4种,分别是(1,1),(2,2),(3,3),(4,4),
所以,两次着地的面点数相同的概率为 ![]() =
= ![]() ;(2)填表如下:
;(2)填表如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 | 0.25 | 0.25 |
由各组实验的频率可估计“标号1的面着地”的概率是0.25.
(1)根据题意先在表格内列举出所有情形,再用两次着地的面点数相同的情况数除以总情况数即可;(2)用“标号1”的面着地的次数除以试验总次数得到“标号1”的面着地的频率,再利用频率估计概率即可估计“标号1的面着地”的概率.


科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
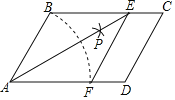
【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
求证:四边形ABEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,OC⊥OB,按下列要求利用量角器过点O作出射线OD、OE;
(1)在图①中作出射线OD满足∠COD=50°,并直接写出∠AOD的度数是 ;
(2)在图②中作出射线OD、OE,使得OD平分∠AOC,OE平分∠BOD,并求∠COE的度数;
(3)如图③,若射线OD从OA出发以每秒10°的速度绕点O顺时针方向旋转,同时射线OE从OC出发以每秒5°的速度绕点O顺时针方向旋转,设旋转的时间为t秒,在旋转过程中,当OB第一次恰好平分∠DOE时,求出t的值,并作出此时OD、OE的大概位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
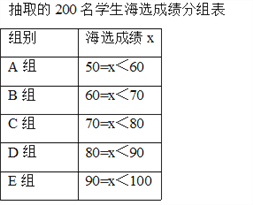
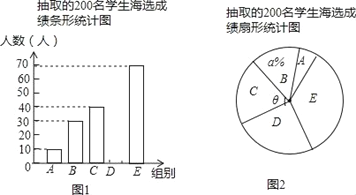
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )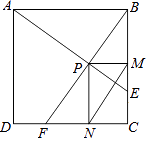
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com