
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).

【答案】(1)见解析;(2)四边形MENF是菱形.(3)2:1.
【解析】试题分析:(1)根据SAS即可证明△ABM≌△DCM;(2)由(1)得出BM=CM,再根据三角形的中位线定理得出EN=MF,EM=FN,先证四边形MENF是平行四边形,再证ME=MF,从而可得平行四边形MENF是菱形;(3)当AD∶AB=2∶1时,四边形MENF是正方形.可以利用正方形的性质得到MA=AB=MD,从而确定AD:AB的值.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,∴AM=DM,
在△ABM和△DCM,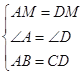
∴△ABM≌△DCM(SAS);
答:四边形MENF是菱形.
证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,![]() ,
,
∴NE=FM,NE∥FM,∴四边形MENF是平行四边形,
∵△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
解:当AD∶AB=2∶1时,四边形MENF是正方形.理由是:
∵四边形MENF是正方形,
∴∠EMF=90°,
由(1)知:Rt△ABM≌Rt△DCM(SAS),
∴∠AMB=∠DMC=45°,
此时MA=MD=DC,
∴AD=2DC,即AD∶AB=2∶1.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C是AB的中点,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x秒(x>0).
(1)当x= 秒时,点P到达点A;
(2)运动过程中点P表示的数是 (用含x的代数式表示);
(3)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,按下列要求画图:
(1)过点A作线段BC的平行线;
(2)将线段BC绕C点按逆时针方向旋转90°得线段EC;
(3)画以BC为一边的正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 , 衍生直线的解析式是;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
![]()
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班准备购买大课间活动器材呼啦圈和跳绳,已知购买1根跳绳和2个呼啦圈要35元,购买2根跳绳和1个呼啦圈要25元.
(1)求每根跳绳、每个呼啦圈各多少元?
(2)根据班级实际情况,需购买跳绳和呼啦圈的总数量为30,总费用不超过300元,但不低于280元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com