
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
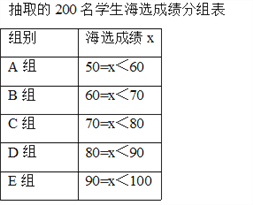
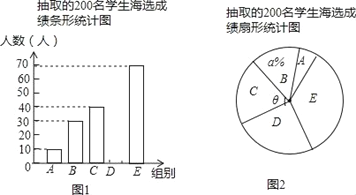
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
【答案】(1)把条形统计图补充完整见解析;(2)72;(3)该校参加这次海选比赛的2000名学生中成绩“优等”的有700人.
【解析】分析:(1)用随机抽取的总人数减去A、B、C、E组的人数,求出D组的人数,从而补全统计图;
(2)用B组抽查的人数除以总人数,即可求出a;用360乘以C组所占的百分比,求出C组扇形的圆心角θ的度数;
(3)用该校参加这次海选比赛的总人数乘以成绩在90分以上(包括90分)所占的百分比,即可得出答案.
详解:(1)D的人数是:200﹣10﹣30﹣40﹣70=50(人),补图如下:
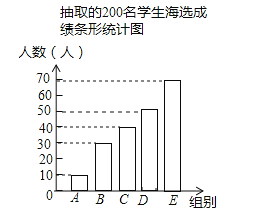
(2)B组人数所占的百分比是![]() ×100%=15%,则a的值是15;
×100%=15%,则a的值是15;
C组扇形的圆心角θ的度数为360×![]() =72°;
=72°;
故答案为:15,72;
(3)根据题意得:2000×![]() =700(人).
=700(人).
答:估计该校参加这次海选比赛的2000名学生中成绩“优等”的有700人.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
![]()
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,右下表是调控后的价目表.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据你的经验,分别求下列事件的概率:
(1)在一个不透明的袋中装有红球3个,白球2个,黑球1个,每种球除颜色外其余都相同,摇匀后随机地从袋中取出1个球,取到红球的概率.
(2)投掷一枚普通正方体骰子,出现的点数为7的概率.
(3)投掷两枚普通硬币,出现两个正面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
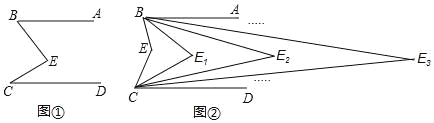
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=![]() ∠BEC;
∠BEC;
(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com