
【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,右下表是调控后的价目表.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?

【答案】⑴ 20元;9.5吨;⑵10.25吨;⑶ 11月交16元、12月交36元或11月交36元、12月交16元.
【解析】
试题(1)因为用水量为8 吨,所以计算单价分为两段,列式计算即可;先计算用水量为6吨和10吨的总价,与26对比,发现9月份用水量x的取值范围,从而列出方程求解;
(2)由题意得出水费30元,用水量超过了10吨,列方程求未知数即可;
(3)设该户居民11月用水量为x吨,12月用水量为(18-x)吨;共交水费52元.列方程求解即可.
试题解析:(1)6×2+(8-6)×4=20,
答:该用户8月应交水费20元;
设该用户9月份用水量为x吨,
2×6=12,2×6+(10-6)×4=28,
∵12<26<28,
∴6<x<10,
则6×2+4(x-6)=26,
x=9.5,
答:该用户9月份用水量为9.5吨;
(2)该用户10月份用水量为y吨,则y>10,
根据题意得:6×2+(10-6)×4+8(y-10)=30,
y=10.25;
(3)设11月份用水x吨,12月份用水y吨,
①当11月份用水不超过6吨时,12月份用水超过10吨时,由题意得:
![]()
解得:![]() (舍去)
(舍去)
②当11月份用水超过6吨不超过10时,12月份用水超过10吨时,由题意得:
![]()
解得:![]()
故11月份的水费为:6×2+1×4=16(元);
12月份的水费为:6×2+4×4+1×8=36(元);
同理可得:11月交36元、12月交16元.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为4cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在一条笔直的公路上有M、P、N三个地点,M、P两地相距20km,甲开汽车,乙骑自行车分别从M、P两地同时出发,匀速前往N地,到达N地后停止运动.已知乙骑自行车的速度为20km/h,甲,乙两人之间的距离y(km)与乙行驶的时间t(h)之间的关系如图②所示. 
(1)M、N两地之间的距离为km;
(2)求线段BC所表示的y与t之间的函数表达式;
(3)若乙到达N地后,甲,乙立即以各自原速度返回M地,请在图②所给的直角坐标系中补全函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成). 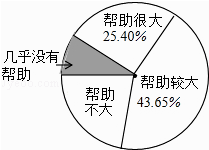
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 543 | 269 | b |
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,OC⊥OB,按下列要求利用量角器过点O作出射线OD、OE;
(1)在图①中作出射线OD满足∠COD=50°,并直接写出∠AOD的度数是 ;
(2)在图②中作出射线OD、OE,使得OD平分∠AOC,OE平分∠BOD,并求∠COE的度数;
(3)如图③,若射线OD从OA出发以每秒10°的速度绕点O顺时针方向旋转,同时射线OE从OC出发以每秒5°的速度绕点O顺时针方向旋转,设旋转的时间为t秒,在旋转过程中,当OB第一次恰好平分∠DOE时,求出t的值,并作出此时OD、OE的大概位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 . 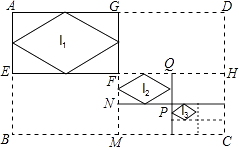
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
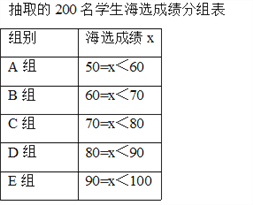
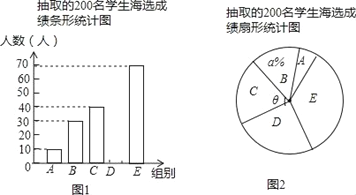
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com