
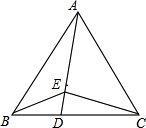
 如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.
如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$. 分析 将△BCE绕点C顺时针旋转60°,作DF∥CE,可得DF∥CE∥AE′,证得△BDF∽BCE,可得EF的长,由△DFE∽△AE′E,利用相似三角形的性质可得结果.
解答 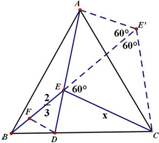 解:将△BCE绕点C顺时针旋转60°,作DF∥CE,
解:将△BCE绕点C顺时针旋转60°,作DF∥CE,
∵将△BCE绕点C顺时针旋转60°得到△ACE′,
∴BE=AE′,∠AE′C=120°,CE=CE′,
∵DF∥CE,∠BEC=120°,
∴∠CEE′=60°,
∴△CEE′为等边三角形,
∴∠CE′E=60°,EE′=CE,
∴∠AE′B=60°,
∴CE∥AE′,∵DF∥CE,
∴DF∥AE′,
∴△BDF∽BCE,
∴$\frac{BF}{BE}$=$\frac{DF}{CE}=\frac{BD}{BC}=\frac{1}{3}$,
∵BE=1,
∴BF=$\frac{1}{3}$,EF=$\frac{2}{3}$,
设CE=x,
∴DF=$\frac{x}{3}$,
∵△DFE∽△AE′E,
∴$\frac{EF}{EE′}=\frac{DF}{AE′}$=$\frac{\frac{x}{3}}{1}$=$\frac{x}{3}$,
∴$\frac{\frac{2}{3}}{x}=\frac{x}{3}$,
解得:x=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查了旋转的性质,等边三角形的性质,相似三角形的性质及判定,将△BCE绕点C顺时针旋转60°,作DF∥CE,得等边三角形和相似三角形是解答此题的关键.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
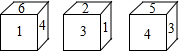 有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )
有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )| A. | 3 | B. | 7 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
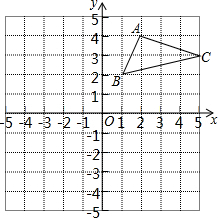 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com