
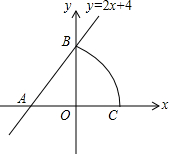 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为$(2\sqrt{5}-2,0)$.
如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为$(2\sqrt{5}-2,0)$. 分析 先根据坐标轴上点的坐标特征得到A(-2,0),B(0,4),再利用勾股定理计算出AB=2$\sqrt{5}$,然后根据圆的半径相等得到AC=AB=2$\sqrt{5}$,进而解答即可.
解答 解:当y=0时,2x+4=0,解得x=-2,则A(-2,0);
当x=0时,y=2x+4=4,则B(0,4),
所以AB=$\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$,
因为以点A为圆心,AB为半径画弧,交x轴于点C,
所以AC=AB=2$\sqrt{5}$,
所以OC=AC-AO=2$\sqrt{5}$-2,
所以的C的坐标为:$(2\sqrt{5}-2,0)$,
故答案为:$(2\sqrt{5}-2,0)$
点评 本题考查了一次函数图象上点的坐标特征,关键是根据一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知三个点A,B,C.按要求完成下列问题:
如图,已知三个点A,B,C.按要求完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
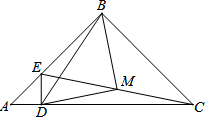 已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.
已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )| A. | 两点之间,线段最短 | B. | 两点确定一条直线 | ||
| C. | 两点之间,直线最短 | D. | 两点确定一条线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,将正比例函数y=-2x的图象沿y轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
在平面直角坐标系xOy中,将正比例函数y=-2x的图象沿y轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com