
【题目】矩形中![]() ,点
,点![]() 分别在边
分别在边![]() 上,点
上,点![]() 分别在边
分别在边![]() 上,
上,![]() 与
与![]() 交于点
交于点![]() ,记
,记![]() .
.
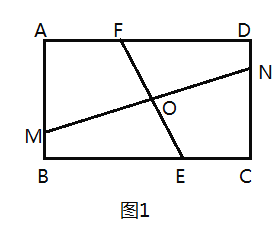
(1)如图1,当![]() 时,若
时,若![]() ,求
,求![]() 的值;
的值;
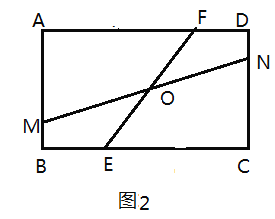
(2)如图2,当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(3)若![]() 的值为3,当
的值为3,当![]() 与
与![]() 重合且
重合且![]() 为直角三角形时,直接写出
为直角三角形时,直接写出![]() 的值.
的值.
【答案】(1)2;(2)当![]() 的长取最大时,
的长取最大时,![]() 取最短,此时
取最短,此时![]() 最大,最大值为
最大,最大值为![]() ;当
;当![]() 的最短时,
的最短时,![]() 的值取最大,此时
的值取最大,此时![]() 的值最小,最小值为
的值最小,最小值为![]() ;(3)
;(3)![]() 为
为![]() 或
或![]()
【解析】
(1)作![]() 于
于![]() 于
于![]() ,设
,设![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() ,得
,得![]() ,进而即可求解;
,进而即可求解;
(2)设![]() ,则
,则![]() ,可得MN最短为
,可得MN最短为![]() ,最长为
,最长为![]() ,EF最短为
,EF最短为![]() ,最长为
,最长为![]() ,进而即可得到结论;
,进而即可得到结论;
(3)当![]() 与
与![]() 重合且
重合且![]() 为直角三角形时,分两种情况:①∠DFO=90°时,②当∠DOF=90°时,分别求解,即可.
为直角三角形时,分两种情况:①∠DFO=90°时,②当∠DOF=90°时,分别求解,即可.
(1)作![]() 于
于![]() 于
于![]() ,设
,设![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ;
;
(2)![]() ,
,
∴设![]() ,则
,则![]() ,
,
![]() 时,MN最短为
时,MN最短为![]() 与对角线重合时,MN最长为
与对角线重合时,MN最长为![]() ,
,
![]() 时,EF最短为
时,EF最短为![]() 与对角线重合时,EF最长为
与对角线重合时,EF最长为![]() ,
,
![]() ,
,
![]() 当
当![]() 的长取最大时,
的长取最大时,![]() 取最短,此时
取最短,此时![]() 最大,最大值为
最大,最大值为![]() ,
,
当![]() 的最短时,
的最短时,![]() 的值取最大,此时
的值取最大,此时![]() 的值最小,最小值为
的值最小,最小值为![]()
即![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ;
;
(3)∵![]() =3,
=3,
∴设EF=a,则MN=3a,
当![]() 与
与![]() 重合且
重合且![]() 为直角三角形时,分两种情况:
为直角三角形时,分两种情况:
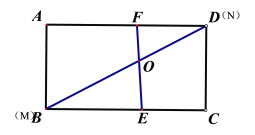
①∠DFO=90°时,AB=CD=EF=a,BD=MN=3a,
∴BC=![]() ,
,
∴![]() =a:
=a:![]() =
=![]() ;
;
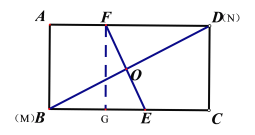
②当∠DOF=90°时,过点F作FG⊥BC于点G,
∴∠EFG+∠FEG=∠DBC+∠FEG,
∴∠EFG=∠DBC,
∵∠FGE=∠BCD=90°,
∴FGE~BCD,
∴![]() ,
,
∵FG=AB,
∴![]() =
=![]() ,
,
综上所述:![]() 为
为![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
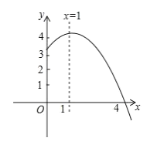
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字2、3、4、6的乒乓球,它们的形状、大小、颜色、质地完全相同,耀华同学先从盒子里随机取出一个小球,记为数字x,不放回,再由洁玲同学随机取出另一个小球,记为数字y,
(1)用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;
(2)求取出的坐标(x,y)对应的点落在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
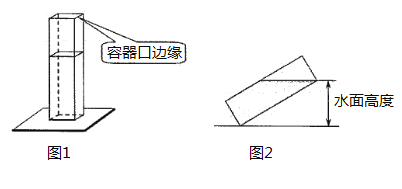
【题目】如图1,长、宽均为![]() 高为
高为![]() 的长方体容器,放置在水平桌面上,里面盛有水,水面高为
的长方体容器,放置在水平桌面上,里面盛有水,水面高为![]() ,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为___________.
,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A1B1C1是位似图形.在网格上建立平面直角坐标系,使得点A的坐标为(1,﹣6).
(1)在图上标出点,△ABC与△A1B1C1的位似中心P.并写出点P的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2,并写出点C2的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
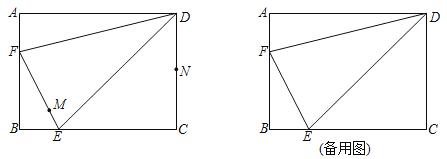
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E,F分别在边BC,AB上,AF=BE=2,连结DE,DF.动点M在EF上从点E向终点F匀速运动,同时,动点N在射线CD上从点C沿CD方向匀速运动,当点M运动到EF的中点时,点N恰好与点D重合,点M到达终点时,M,N同时停止运动.
(1)求EF的长.
(2)设CN=x,EM=y,求y关于x的函数表达式,并写出自变量x的取值范围.
(3)连结MN,当MN与△DEF的一边平行时,求CN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com