
(本小题满分11分)已知关于x的函数y=m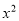 -x-(m-1).
-x-(m-1).
(1)m=__________时,y=m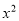 -x-(m-1)是一次函数;
-x-(m-1)是一次函数;
(2)求证:对任何实数m,y=m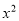 -x-(m-1)的图像与
-x-(m-1)的图像与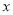 都有公共点;
都有公共点;
(3)若是关于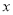 的二次函数y=m
的二次函数y=m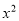 -x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
-x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,y=m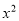 -x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
-x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
(1)m=0;(2)见解析;(3)m=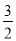 ,或m=-
,或m=- ;(4)(1,0)或(-1,2).
;(4)(1,0)或(-1,2).
【解析】
试题分析:(1)根据一次函数的定义进行求解;(2)分一次函数和二次函数两种情况进行讨论计算;(3)首先求出A、B两点的坐标,然后求出AB的长度以及顶点的纵坐标,根据等腰直角三角形的性质得出AB=2×顶点的纵坐标,求出m的值;(4)首先去m=0和m=1将函数化成简单的一次函数和二次函数,然后求出它们的交点坐标,将交点坐标分别代入解析式,看是否符合解析式,如果符合就是点P.
试题解析:(1)根据题意得:m=0
(2)m=0 时,y=-x+1与x轴交于点(1,0)
M≠0时,△=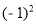 +4m(m-1)=
+4m(m-1)=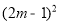 ≥0
≥0
∴对任何实数m,y=m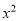 -x-(m-1)的图像与x都有公共点;
-x-(m-1)的图像与x都有公共点;
(3) 由m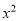 -x-(m-1)=0得
-x-(m-1)=0得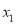 =1,
=1, ∴AB=
∴AB=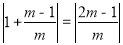
且顶点C的纵坐标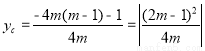
∵△ABC是等腰直角三角形
∴AB=2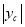 即
即
∴m= 或m=
或m=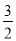 ,或m=-
,或m=-
经检验m=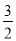 ,或m=-
,或m=-
(4)由m=0得y=-x+1, m=1得y=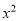 -x
-x
由 解得
解得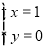 或
或
对任何实数m
当x=1时,y=m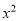 -x-(m-1)=m-1-(m-1)=0
-x-(m-1)=m-1-(m-1)=0
当x=-1时,y=m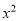 -x-(m-1)=m+1-(m-1)=2
-x-(m-1)=m+1-(m-1)=2
对任何实数m,y=m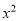 -x-(m-1)的图像都经过点(1,0)(-1,2)
-x-(m-1)的图像都经过点(1,0)(-1,2)
即所求点P的坐标为(1,0)或(-1,2)
考点:二次函数的性质、一次函数的性质、等腰三角形的性质.
考点分析: 考点1:一次函数 函数的定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
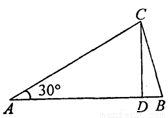
如图,在顶角为30°的等腰△ABC中,AB=AC,若过点C作CD⊥AB于点D.根据图形计算tan∠BCD= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:填空题
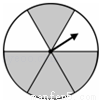
如图,一个圆形转盘被分成6个圆心角都为60°的扇形,任意转动这个转盘1次,当转盘停止转动时,指针指向阴影区域的概率是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:选择题
一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )

A.和 B.谐 C.东 D.台
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:解答题
(本小题满分6分)在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
(1)如图,直线y=-2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
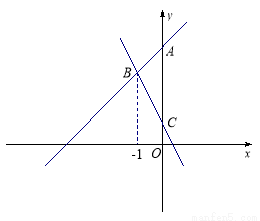
①求点B的坐标及k的值;
②直线y=-2x+1、直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(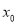 ,0),若-2<
,0),若-2<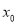 <-1,求k的取值范围.
<-1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:选择题
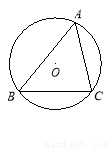
如图,△ABC内接于半径为5的⊙O,BC=8.则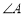 的正切值等于 ( )
的正切值等于 ( )
A.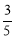 B.
B.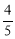 C.
C.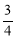 D.
D.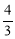
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:解答题
(共8分)一个生产小组某种零件,计划30天完成,若每天多生产5个,则26天完成且比原计划多生产10个零件,问原计划每天生产多少个?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省邯郸市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )

A.函数有最小值
B.对称轴是直线x=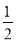
C.当x<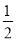 时,y随x的增大而减小
时,y随x的增大而减小
D.当 -1<x<2时,y>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com