
科目:初中数学 来源: 题型:解答题
 如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)
如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题.
小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
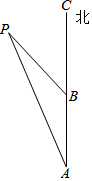 如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.
如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
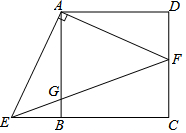 如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.
如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
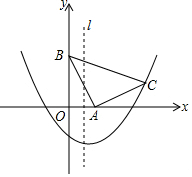 如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=$\frac{1}{2}$x2+bx-2的图象过C点.
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=$\frac{1}{2}$x2+bx-2的图象过C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
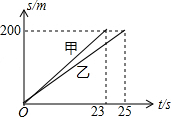 如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:
如图所示的是甲、乙两人在争夺冠军中的比赛图,其中t表示赛跑时所用时间,s表示赛跑的距离,根据图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com