
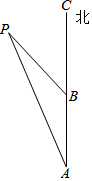
 如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.
如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.  手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
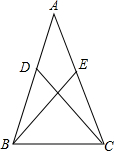 如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性.
如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k<0,b<0 | C. | k<0,b>0 | D. | k>0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
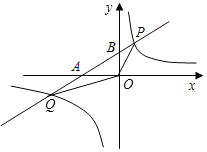 如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=$\frac{1}{2}$.
如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com