
【题目】如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论:①∠AMD=90°;②M为BC的中点;③AB+CD=AD;④S△ADM=S梯形ABCD;⑤M到AD的距离等于BC的一半.其中正确的结论有____

【答案】①②③⑤.
【解析】
作MN⊥AD于N,如图,根据角平分线的性质得MB=MN,MN=MC,则根据“HL”可证明Rt△MCD≌Rt△MND,Rt△MBA≌Rt△MNA,则∠1=∠2,∠3=∠4,再利用平角的定义可得∠AMD=90°,则可对①进行判断;同时利用MB=MN=MC可对②⑤进行判断;根据全等三角形的性质,利用Rt△MCD≌Rt△MND,Rt△MBA≌Rt△MNA得到CD=ND,AB=AN,则可对③进行判断;根据全等三角形性质得S△MCD=S△MND,S△MBA=S△MNA,所以S△ADM=![]() S梯形ABCD,则可对④进行判断.
S梯形ABCD,则可对④进行判断.
过点M作MN⊥AD交AD于N,如图,

∵AM和DM分别为∠DAB与∠ADC的平分线,
且MN⊥AD,MC⊥CD,MB⊥AB,
∴MB=MN,MN=MC,∴MB=MN=MC,
∴MB=MC,所以②⑤正确;
在Rt△MCD和Rt△MND中
![]() ,
,
∴Rt△MCD≌Rt△MND,
∴∠1=∠2,
同理可得Rt△MBA≌Rt△MNA,
∴∠3=∠4,
∴∠2+∠4=![]() ∠CMN+
∠CMN+![]() ∠BMN=90°,
∠BMN=90°,
即∠AMD=90°,所以①正确;
∵Rt△MCD≌Rt△MND,Rt△MBA≌Rt△MNA,
∴CD=ND,AB=AN,
∴AD=AN+ND=AB+CD,所以③正确;
∵Rt△MCD≌Rt△MND,Rt△MBA≌Rt△MNA,
∴S△MCD=S△MND,S△MBA=S△MNA,
∴S△ADM=![]() S梯形ABCD,所以④错误.
S梯形ABCD,所以④错误.
故答案为①②③⑤.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为S,作△ABC边中线AC1,取AB的中点A1,连接A1C1得到第一个三角形△A1BC1,作△A1BC1中线A1C2,取A1B的中点A2,连接A1C2得到第二个三角形△A2BC2………,重复这样的操作,则第2019个三角形△A2019BC2019的面积是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论是( )
.其中正确结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形纸片![]() 中,
中,![]() ,折叠纸片,使得点
,折叠纸片,使得点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,点
,点![]() 分别在边
分别在边![]() 和
和![]() 上,当点
上,当点![]() 恰好是
恰好是![]() 边的中点时,点
边的中点时,点![]() 与点
与点![]() 重合,若在折叠过程中
重合,若在折叠过程中![]() ,则
,则![]() 等于________
等于________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 AD//BC, 点 E 为 CD 上一点,AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证:(1)△ABE≌△AEF;(2) AD+BC=AB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D,E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=9cm,DE=3cm,则BC的长为 ( )

A.12cmB.11cmC.9cmD.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
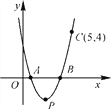
【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类:![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.

根据以上信息,解答下列问题:
(1)![]() 类学生有_________人,补全条形统计图;
类学生有_________人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的__________%;
类学生人数占被调查总人数的__________%;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com