
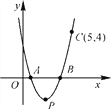
【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
【答案】(1) (![]() ,-
,- ![]() );(2)答案不唯一,合理即可,y=x2+x+2.
);(2)答案不唯一,合理即可,y=x2+x+2.
【解析】试题分析:将点c坐标代入函数表达式即可求出a的值,a=1,将函数表达式转换为顶点式y=x2-5x+4=(x-![]() )2-
)2-![]() ,所以顶点坐标是(
,所以顶点坐标是(![]() ,-
,- ![]() );将抛物线平移后顶点在第二象限,答案不唯一,可通过平移顶点,例如先向左平移3个单位长度,则变为y= (x-
);将抛物线平移后顶点在第二象限,答案不唯一,可通过平移顶点,例如先向左平移3个单位长度,则变为y= (x-![]() )2-
)2-![]() ,再向上平移4个单位,得到y= (x-
,再向上平移4个单位,得到y= (x-![]() )2-
)2-![]() +4= (x+
+4= (x+![]() )2+
)2+![]() = x2+x+2.
= x2+x+2.
解:(1)把点C(5,4)代入抛物线y=ax2-5ax+4a,得25a-25a+4a=4.解得a=1.
∴二次函数的表达式为y=x2-5x+4.
∵y=x2-5x+4=(x-![]() )2-
)2-![]() ,
,
∴顶点P的坐标为(![]() ,-
,- ![]() ).
).
(2)答案不唯一,合理即可,如:先向左平移3个单位长度,再向上平移4个单位长度,得到的二次函数表达式为y=(x-![]() +3)2-
+3)2-![]() +4=(x+
+4=(x+![]() )2+
)2+![]() ,
,
即y=x2+x+2.


科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(每个学生必选且只能选一门课程)班主任想要了解全班同学对哪门课程感兴趣,就在全班进行调查,将获得的数据整理绘制成如图下所示两幅不完整的统计图.
学习感兴趣的课程情况条形统计图:

学习感兴趣的课程情况扇形统计图:
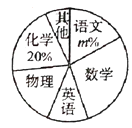
根据统计图信息,解答下列问题.
(1)全班共有________名学生,![]() 的值是________
的值是________
(2)据以上信息,补全条形统计图.
(3)扇形统计图中,“数学”所在扇形的圆心角是________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩(成绩取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题:
(1)m=______,n=_____.
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个正方形甲和两个正方形乙分别沿着图中虚线川剪刀剪成4个完全相等的长方形和一个正方形(如图1),已知正方形甲中剪出的小正方形面积是1,正方形乙中剪出的小正方形面积是4,现将剪得的12个长方形摆成如图2正方形![]() (不重叠无缝隙).则正方形
(不重叠无缝隙).则正方形![]() 的面积是()
的面积是()
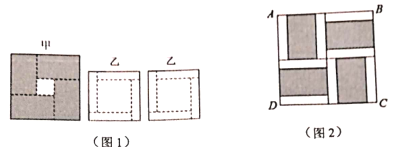
A.9B.16C.25D.36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,连接![]() ,求证:
,求证:![]() ;
;

(2)如图2,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点N,
于点N,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 在直线
在直线![]() 的右侧作
的右侧作![]() 且
且![]()
![]() 为线段
为线段![]() 的中点,当点
的中点,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,写出点
时,写出点![]() 运动的路径长并简要说明理由.
运动的路径长并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列事件发生的可能性,并标在图中的大致位置上.
(1)袋中有10个红球,摸到红球;
(2)袋中有10个红球,摸到白球;
(3)一副混合均匀的扑克牌(除去大、小王),从中任意抽取一张,这一张恰好是A;
(4)一个布袋中有2个黑球和2个白球,从中任意摸出一个球,恰好是黑球;
(5)任意掷出一个质地均匀的骰子(每个面上分别标有数字1,2,3,4,5,6),朝上一面的数字大于2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com