
【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

【答案】(1)10°;(2)![]() (∠C-∠B).
(∠C-∠B).
【解析】
(1)在三角形ABC中,由∠B与∠C的度数求出∠BAC的度数,根据AE为角平分线求出∠BAE的度数,由∠BAD-∠B即可求出∠DAE的度数;
(2)仿照(1)得出∠DAE与、∠B、∠C的数量关系即可.
(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
又∵AE是△ABC的角平分线,
∴∠BAE=![]() ∠BAC=50°,
∠BAC=50°,
∵AD是△ABC的高,
∴∠BAD=90°-∠B=90°-30°=60°,
则∠DAE=∠BAD-∠BAE=10°,
故答案为:10°;
(2)∠DAE=![]() (∠C-∠B),
(∠C-∠B),
理由如下:∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∵AE是△ABC的角平分线,
∴∠EAC=![]() ∠BAC,
∠BAC,
∵∠BAC=180°-∠B-∠C
∴∠DAE=∠EAC-∠DAC,
=![]() ∠BAC-(90°-∠C),
∠BAC-(90°-∠C),
=![]() (180°-∠B-∠C)-90°+∠C,
(180°-∠B-∠C)-90°+∠C,
=90°-![]() ∠B-
∠B-![]() ∠C-90°+∠C,
∠C-90°+∠C,
=![]() (∠C-∠B).
(∠C-∠B).
故答案为:![]() (∠C-∠B).
(∠C-∠B).


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
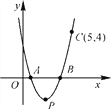
【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,∠1+∠2=180°,∠A=∠C,试说明:AE∥BC.
解:因为∠1+∠2=180°,
所以AB∥ (同旁内角互补,两直线平行)
所以∠A=∠EDC( ),
又因为∠A=∠C(已知)
所以∠EDC=∠C(等量代换),
所以AE∥BC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:

(1)A,B两城相距多少千米?
(2)分别求甲、乙两车离开A城的距离y与x的关系式.
(3)求乙车出发后几小时追上甲车?
(4)求甲车出发几小时的时候,甲、乙两车相距50千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
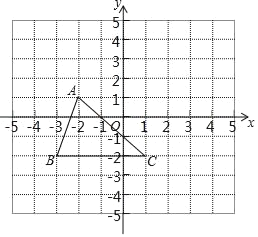
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'
(1)在图中画出△A′B′C';
(2)写出A',B'的坐标;
(3)求出△COC′的面积;
(4)在y轴上是否存在一点P,使得△BCP与△ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程
例:若代数式![]() 的值是
的值是![]() ,求
,求![]() 的取值范围.
的取值范围.
解:原式=![]()
当![]() 时,原式
时,原式![]() ,解得
,解得![]() (舍去);
(舍去);
当![]() 时,原式
时,原式![]() ,符合条件;
,符合条件;
当![]() 时,原式
时,原式![]() ,解得
,解得 ![]() (舍去).
(舍去).
所以,![]() 的取值范围是
的取值范围是![]()
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
![]() 当
当![]() 时,化简:
时,化简:![]()
![]() 若等式
若等式![]() 成立,则
成立,则![]() 的取值范围是
的取值范围是
![]() 若
若![]() ,求
,求![]() 的取值.
的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com