
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:

(1)A,B两城相距多少千米?
(2)分别求甲、乙两车离开A城的距离y与x的关系式.
(3)求乙车出发后几小时追上甲车?
(4)求甲车出发几小时的时候,甲、乙两车相距50千米?
【答案】(1)300千米;(2)甲对应的函数解析式为:y=60x,乙对应的函数解析式为y=100x100;(3)1.5 ;(4)![]() 小时、1.25小时、3.75小时、
小时、1.25小时、3.75小时、![]() 小时时,甲、乙两车相距50千米
小时时,甲、乙两车相距50千米
【解析】
(1)根据函数图象可以解答本题;
(2)根据图象中的信息分别求出甲乙两车对应的函数解析式,
(3)根据(2)甲乙两车对应的函数解析式,然后令它们相等即可解答本题;
(4)根据(2)中的函数解析式,可知它们相遇前和相遇后两种情况相距50千米,从而可以解答本题.
(1)由图可知,
A、B两城相距300千米;
(2)设甲对应的函数解析式为:y=kx,
300=5k
解得,k=60,
即甲对应的函数解析式为:y=60x,
设乙对应的函数解析式为y=mx+n,
![]() ,
,
解得,![]() ,
,
即乙对应的函数解析式为y=100x100,
(3)解![]() ,解得
,解得![]()
2.51=1.5,
即乙车出发后1.5小时追上甲车;
(4)由题意可得,
当乙出发前甲、乙两车相距50千米,则50=60x,得x=![]() ,
,
当乙出发后到乙到达终点的过程中,则60x(100x100)=±50,
解得,x=1.25或x=3.75,
当乙到达终点后甲、乙两车相距50千米,则30050=60x,得x=![]() ,
,
即![]() 小时、1.25小时、3.75小时、
小时、1.25小时、3.75小时、![]() 小时时,甲、乙两车相距50千米.
小时时,甲、乙两车相距50千米.


科目:初中数学 来源: 题型:
【题目】将一个正方形甲和两个正方形乙分别沿着图中虚线川剪刀剪成4个完全相等的长方形和一个正方形(如图1),已知正方形甲中剪出的小正方形面积是1,正方形乙中剪出的小正方形面积是4,现将剪得的12个长方形摆成如图2正方形![]() (不重叠无缝隙).则正方形
(不重叠无缝隙).则正方形![]() 的面积是()
的面积是()
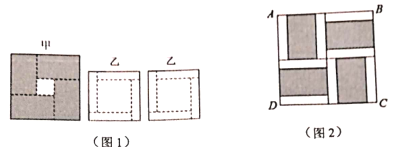
A.9B.16C.25D.36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
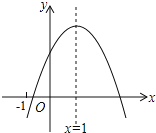
A.abc<0 B.2a+b=0 C.b2﹣4ac>0 D.a﹣b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据所给信息,回答下列问题.
买![]() 一共要170元,
一共要170元,
买![]() 一共要110元.
一共要110元.
(1)分别求出桌子和椅子的单价是多少?
(2)学校根据实际情况,要求购买桌椅总费用不超过1000元,且购买桌子的数量是椅子数量的![]() ,求该校本次购买桌子和椅子共有哪几种方案?
,求该校本次购买桌子和椅子共有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,直线AB与a,b分别相交于点A,B,AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求a与b的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△A1A2A3,△A3A4A5,△A5A6A7,△A7A8A9,…,都是等腰直角三角形,且点A1,A3,A5,A7,A9的坐标分别为A1 (3,0),A3 (1,0),A5 (4,0),A7 (0.0),A9 (5.0),依据图形所反映的规律,则A102的坐标为( )

A. (2,25)B. (2,26)C. (![]() ,﹣
,﹣![]() )D. (
)D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
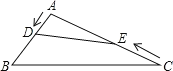
A. 4或4.8 B. 3或4.8 C. 2或4 D. 1或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班决定购买一些笔记本和文具盒做奖品.已知需要的笔记本数量是文具盒数量的3倍,购买的总费用不低于220元,但不高于250元.
(1)商店内笔记本的售价4元/本,文具盒的售价为10元/个,设购买笔记本的数量为x,按照班级所定的费用,有几种购买方案?每种方案中笔记本和文具盒数量各为多少?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)经过还价,老板同意4元/本的笔记本可打八折,10元/个的文具盒可打七折,用(2)中的最少费用最多还可以多买多少笔记本和文具盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com