
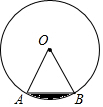
 如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积.
如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积. 科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形对应角相等 | |
| B. | 如果实数x满足x2>0,那么x≠0 | |
| C. | 如果两个角相等,那么它们是对顶角 | |
| D. | 对顶角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
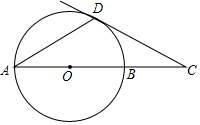 如图1,⊙O的直径AB=2,⊙O的切线CD与AB的延长线交于点C,D为切点,∠C=30°,则AD等于( )
如图1,⊙O的直径AB=2,⊙O的切线CD与AB的延长线交于点C,D为切点,∠C=30°,则AD等于( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$-\frac{1}{2}$x2+bx+c与x轴交于A,B两点,与y轴交于点C,已知A(-1,0),B(4,0),点D(m,n)是线段BC上的一个动点(点D不与B,C重合),过点D作x轴的垂线与抛物线相交于点F,垂足为E.
如图,抛物线y=$-\frac{1}{2}$x2+bx+c与x轴交于A,B两点,与y轴交于点C,已知A(-1,0),B(4,0),点D(m,n)是线段BC上的一个动点(点D不与B,C重合),过点D作x轴的垂线与抛物线相交于点F,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )
如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图某防汛大堤的横断面为梯形ABCD,斜坡AB的坡度i1=1:1.5,斜坡CD的坡度i2=1:1,大堤顶高AD为10米,为了增强抗洪能力,现将大堤加高,加高部分的横截面为梯形ADFE,AD∥EF,且点E、F分别在BA、CD的延长线上,新坝顶宽EF为7.5米,求大堤加高了多少米?
如图某防汛大堤的横断面为梯形ABCD,斜坡AB的坡度i1=1:1.5,斜坡CD的坡度i2=1:1,大堤顶高AD为10米,为了增强抗洪能力,现将大堤加高,加高部分的横截面为梯形ADFE,AD∥EF,且点E、F分别在BA、CD的延长线上,新坝顶宽EF为7.5米,求大堤加高了多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com