
 ��ͼ��������y=$-\frac{1}{2}$x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����֪A��-1��0����B��4��0������D��m��n�����߶�BC�ϵ�һ�����㣨��D����B��C�غϣ�������D��x��Ĵ������������ཻ�ڵ�F������ΪE��
��ͼ��������y=$-\frac{1}{2}$x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����֪A��-1��0����B��4��0������D��m��n�����߶�BC�ϵ�һ�����㣨��D����B��C�غϣ�������D��x��Ĵ������������ཻ�ڵ�F������ΪE������ ��1���ѵ�A��-1��0����B��4��0��������ֱ���뺯������ʽ���г�����ϵ��b��c�ķ����飬ͨ���ⷽ����������ǵ�ֵ���ɣ���x=0���ɵõ���C�������ꣻ
��2�����������ε������ʽ�õ�S=-m2+4m����϶��κ�����ֵ�����н��
��3�������������εĶ�Ӧ����ȡ�ƽ����DE��OC�������Լ�������Ǻ����Ķ������m=1�������ã�2���е�$n=-\frac{1}{2}m+2$����n��ֵ����D������꣮
��� �⣺��1���������⣬��$\left\{\begin{array}{l}-\frac{1}{2}-b+c=0\\-8+4b+c=0\end{array}\right.$��
��ã�$\left\{\begin{array}{l}b=\frac{3}{2}\\ c=2\end{array}\right.$��
�������ߵĽ���ʽΪ$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2$��
��x=0ʱ��$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2=2$��
��C��0��2����
��2����DE��x����E��D��m��n����
��$tan��DBE=\frac{DE}{BE}=\frac{OC}{OB}$��
��$\frac{n}{4-m}=\frac{2}{4}$����$n=-\frac{1}{2}m+2$��
��x=mʱ��$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2=-\frac{1}{2}{m^2}+\frac{3}{2}m+2$��
��$DF=��-\frac{1}{2}{m^2}+\frac{3}{2}m+2��-��-\frac{1}{2}m+2��=-\frac{1}{2}{m^2}+2m$��
��${S_{��CBF}}={S_{��CDF}}+{S_{��BDF}}=\frac{1}{2}DF•OE+\frac{1}{2}DF•BE=\frac{1}{2}DF•OB=-{m^2}+4m$����S=-m2+4m��
��-1��0��0��m��4��
�൱$m=-\frac{4}{2����-1��}=2$ʱ��S���ʱ$n=-\frac{1}{2}m+2=1$��
�൱S���ʱD������Ϊ��2��1����
��3�����ڣ��������£�
�ߡ�ECD=��BCE
�൱��CED=��CBEʱ����CDE�ס�CEB��
�ߡ�COB=��DEB=90�㣮
��DE��OC��
���OCE=��CED=��CBE��
��$tan��OCE=\frac{OE}{OC}=\frac{m}{2}$��$tan��CBE=\frac{OC}{BC}=\frac{1}{2}$��
��$\frac{m}{2}=\frac{1}{2}$�����m=1��
��$n=-\frac{1}{2}m+2=\frac{3}{2}$��D��1��$\frac{3}{2}$����
���� ��Ҫ�����˶��κ����Ľ���ʽ�����뼸��ͼ�ν�ϵ��ۺ�������������Ҫ���������ν�ϵ�˼��Ѵ����ͼ���ͼ�ν�����������õ������������ʾ�߶εij��ȣ��Ӷ�����߶�֮��Ĺ�ϵ��


 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���ABC���������������ֱ���A��2��2����B��4��0����C��4��-4����
��ͼ����ƽ��ֱ������ϵ�У���ABC���������������ֱ���A��2��2����B��4��0����C��4��-4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 4 | C�� | -4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
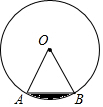 ��ͼ���ڰ뾶Ϊ6�ġ�O�У���AB��Ϊ6������AB��$\widehat{AB}$��Χ�ɵ���Ӱ���ֵ������
��ͼ���ڰ뾶Ϊ6�ġ�O�У���AB��Ϊ6������AB��$\widehat{AB}$��Χ�ɵ���Ӱ���ֵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
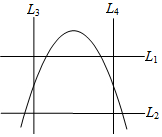 С������ͼ��ˮƽ��l1��l2������һ������x�ᣬ������Ϊ����������ֱ��l3��l4������һ������y�ᣬ������Ϊ�������ڴ�����ƽ���л������κ���y=ax2-2a2x+1��ͼ��������
С������ͼ��ˮƽ��l1��l2������һ������x�ᣬ������Ϊ����������ֱ��l3��l4������һ������y�ᣬ������Ϊ�������ڴ�����ƽ���л������κ���y=ax2-2a2x+1��ͼ��������| A�� | l1Ϊx�ᣬl3Ϊy�� | B�� | l2Ϊx�ᣬl3Ϊy�� | C�� | l1Ϊx�ᣬl4Ϊy�� | D�� | l2Ϊx�ᣬl4Ϊy�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��PA��PB���O�ֱ������ڵ�A����B��AC�ǡ�O��ֱ����PC����O�ڵ�D����֪��APB=60�㣬AC=2����ôAD�ij�Ϊ$\frac{2\sqrt{21}}{7}$��
��ͼ��PA��PB���O�ֱ������ڵ�A����B��AC�ǡ�O��ֱ����PC����O�ڵ�D����֪��APB=60�㣬AC=2����ôAD�ij�Ϊ$\frac{2\sqrt{21}}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com