Question

4．已知，△ABC内接于⊙O，AB=AC，点D在⊙O上，点E在射线DC上且BD=CE，连接AE，BD．
（1）如图1，当点D在弧BC上时，求证：∠ACB=∠AED；
（2）如图2，当点D在弧AB上且点A、O、E三点共线时，求证：DG=EG；
（3）在（2）的条件下，连接AD，∠ABC的平分线交⊙O于点F，若AD=$\frac{7}{2}$，OA=$\frac{25}{4}$，求线段BF的长．

Answer 1

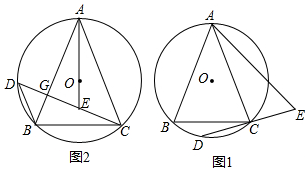
分析 （1）如图1中，连接AD，由△ABD≌△ACE（SAS），推出∠ADB=∠AED，再根据圆周角定理可得∠ADB=∠ACB，由此即可证明．
（2）如图2中，连接BE．首先证明BD=BE=BE，推出∠BDE=∠BED=∠BAC，由∠BED=2∠ECB，推出∠BAC=2∠ECB，推出∠BAE=∠ECB，由∠ABC=∠CBG=90°-∠BAE=90°-∠ECB，推出∠CGB=180°-（∠CBG+∠ECB）=90°，即可证明．
（3）如图3中，延长AE交BC于P，交⊙O于T，连接AF、FC，AD，作EK⊥AB于K，FM⊥BA于M，FN⊥BC于N．首先证明CG=CT，由BC⊥GT，推出PG=PT=$\frac{9}{2}$，AP=$\frac{25}{2}$-$\frac{9}{2}$=8，由△CPA∽△TPC，得CP²=PT•AP=36，推出PB=PC=6，AB=10，Y2∠EBA=∠EBP，EK⊥AB，EP⊥BC，推出EK=EP，由$\frac{{S}_{△ABE}}{{S}_{△EBP}}$=$\frac{\frac{1}{2}•AB•EK}{\frac{1}{2}•PB•EP}$=$\frac{AE}{EP}$，推出$\frac{AE}{EP}$=$\frac{AB}{PB}$=$\frac{5}{3}$，由PA=8，推出AE=5，EP=3，BE=$\sqrt{E{P}^{2}+B{P}^{2}}$=3$\sqrt{5}$，再证明△FBM≌△FBN，Rt△AFM≌Rt△CFN，推出BM=BN，AM=CN，TC BM+BN=AB+AM+BC-CN=AB+BC=22，TC BM=BN=11，AM=CN=1，再由EP∥FM，得$\frac{BF}{BE}$=$\frac{BN}{PB}$，由此即可求出BF．

解答 （1）证明：如图1中，连接AD．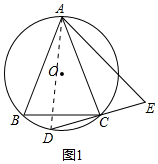

∵AB=AC
∴弧AB=弧AC，
∴∠ABC=∠ACB=∠ADB=∠ADC，
∵∠ABD=∠ACE，BD=CE，
∴△ABD≌△ACE（SAS），
∴∠ADB=∠AED，
∴∠ACB=∠AED．

（2）证明：如图2中，连接BE．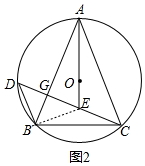

∵AB=AC，A、O、E三点共线，
∴AE垂直平分BC，
∴BE=CE，∠BAE=∠CAE，
∴∠EBC=∠ECB，
∵BD=CE，
∴BD=BE=BE，
∴∠BDE=∠BED=∠BAC，
∵∠BED=2∠ECB，
∴∠BAC=2∠ECB，
∴∠BAE=∠ECB，
∵∠ABC=∠CBG=90°-∠BAE=90°-∠ECB，
∴∠CGB=180°-（∠CBG+∠ECB）=90°，
∴BG⊥DE，
∴DG=EG．

（3）解：如图3中，延长AE交BC于P，交⊙O于T，连接AF、FC，AD，作EK⊥AB于K，FM⊥BA于M，FN⊥BC于N．

∵AB垂直平分线段DG，
∴AD=AG=$\frac{7}{2}$，∵OA=$\frac{25}{4}$，
∴OG=$\frac{25}{4}$-$\frac{7}{2}$=$\frac{11}{4}$，GT=$\frac{25}{2}$-$\frac{7}{2}$=9，
∵∠CGT=∠AGD，∠T=∠ADG，∠ADG=∠AGD，
∴∠CGT=∠T，
∴CG=CT，∵BC⊥GT，
∴PG=PT=$\frac{9}{2}$，AP=$\frac{25}{2}$-$\frac{9}{2}$=8，
由△CPA∽△TPC，得CP²=PT•AP=36，
∴PB=PC=6，
在Rt△APB中，AB=$\sqrt{A{P}^{2}+P{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∵∠EBA=∠EBP，EK⊥AB，EP⊥BC，
∴EK=EP，
∴$\frac{{S}_{△ABE}}{{S}_{△EBP}}$=$\frac{\frac{1}{2}•AB•EK}{\frac{1}{2}•PB•EP}$=$\frac{AE}{EP}$，
∴$\frac{AE}{EP}$=$\frac{AB}{PB}$=$\frac{5}{3}$，
∵PA=8，
∴AE=5，EP=3，BE=$\sqrt{E{P}^{2}+B{P}^{2}}$=3$\sqrt{5}$，
∵BF=BF，∠FBM=∠FBN，∠BMF=∠BNF，
∴△FBM≌△FBN，$\widehat{AF}$=$\widehat{FC}$
∴BM=BN，FM=FN，AF=FC，
∵FM=FN，AF=FC，
∴Rt△AFM≌Rt△CFN，
∴AM=CN，
∴BM+BN=AB+AM+BC-CN=AB+BC=22，
∴BM=BN=11，AM=CN=1，
∵EP∥FM，
∴$\frac{BF}{BE}$=$\frac{BN}{PB}$，
∴$\frac{BF}{3\sqrt{5}}$=$\frac{11}{6}$，
∴BF=$\frac{11\sqrt{5}}{2}$．

点评 本题考查圆综合题、全等三角形的判定和性质、相似三角形的判定和性质、平行线的分线段成比例定理、等腰三角形的判定和性质、勾股定理等知识，解题的关键是学会条件常用辅助线，构造全等三角形，学会用面积法证明线段之间的关系，题目比较难，条件比较多，属于中考压轴题．