练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．如图，点A、B在数轴上，其对应的数分别是-14和10，若点C也在这个数轴上，且AC：BC=2：5，则点C对应的数是-$\frac{50}{7}$或-30．

    分析 设点C表示的数为x，分点C在A、B之间和点C在点A的左边两种情况，利用两点间的距离公式列方程求解可得．

    解答 解：设点C表示的数为x，
    当点C在A、B之间时，$\frac{x+14}{10-x}$=$\frac{2}{5}$，
    解得：x=-$\frac{50}{7}$；
    当点C在点A的左边时，$\frac{-14-x}{10-x}$=$\frac{2}{5}$，
    解得：x=-30，
    故答案为：-$\frac{50}{7}$或-30．

    点评 本题主要考查数轴，熟练掌握两点间的距离公式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．已知，△ABC内接于⊙O，AB=AC，点D在⊙O上，点E在射线DC上且BD=CE，连接AE，BD．
    （1）如图1，当点D在弧BC上时，求证：∠ACB=∠AED；
    （2）如图2，当点D在弧AB上且点A、O、E三点共线时，求证：DG=EG；
    （3）在（2）的条件下，连接AD，∠ABC的平分线交⊙O于点F，若AD=$\frac{7}{2}$，OA=$\frac{25}{4}$，求线段BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列调查适合普查的是（　　）
    A．调查全国初中生的身体素质情况
    B．调查一批蜡烛的使用寿命
    C．调查一架“歼20”隐形战机各部零件的质量
    D．调查我国2012年中央电视台春节联欢晚会的收视率

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点D．
    （1）求BC的长；（2）求弦BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，将△AOB绕点O逆时针方向旋转45°后得到△A′OB′，若∠AOB=10°，则∠AOB′的度数是（　　）
    A．25°B．30°C．35°D．40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．在一个不透明的口袋中，装有若干个红球和6个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.3，则估计盒子中大约有红球（　　）
    A．16个B．14个C．20个D．30个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再化简：$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$÷$\frac{x-2}{{x}^{2}+2x}$-1，其中x=2-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．去分母解关于x的方程$\frac{x-3}{x-2}$=$\frac{m}{x-2}$时产生增根，则m的值为（　　）
    A．m=1B．m=-1C．m=2D．m无法求出

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

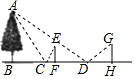    12．某一天，小明和小亮来到一河边，想用平面镜和皮尺测量这条河的大致宽度，两人在确保无安全隐患的情况下，现在河岸边选择了一点C（点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸）．
    小明到F点时正好在平面镜中看到树尖A，小亮在点D放置平面镜，小亮到H点时正好在平面镜中看到树尖A，且F、D、H均在BC的延长线上，小明的眼睛距地面的高度EF=1.5m，小亮的眼睛距地面的高度GH=1.6m，测得CF=1m，DH=2m，CD=8.4m，AB⊥BH，EF⊥BH，GH⊥BH，根据以上测量过程及测量数据，请你求出河宽BC是多少米？

    查看答案和解析>>

    同步练习册答案