
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为 ;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B',补全△A′B′C′;
(3)在图中画出△ABC的高CD;
(4)能使S△ABC=S△QBC的格点Q(A点除外)共有 个.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为

A. 20 cm B. 30 cm C. 0 cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号).①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.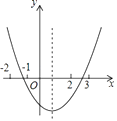
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习几何的一个重要方法就是要学会抓住基本图形,让我们来做一次研究性学习.

(1)如图①所示的图形,像我们常见的学习用品一圆规,我们常把这样的图形叫做“规形图”.请你观察“规形图”,试探究∠BOC与∠A、∠B、∠C之间的关系,并说明理由:
(2)如图②,若△ABC中,BO平分∠ABC,CO平分∠ACB,且它们相交于点O,试探究∠BOC与∠A的关系;
(3)如图③,若△ABC中,∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为 _.
∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为 _.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部![]() , 颖颖的头顶
, 颖颖的头顶![]() 及亮亮的眼睛
及亮亮的眼睛![]() 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置![]() ,
, ![]() . 然后测出两人之间的距离
. 然后测出两人之间的距离![]() , 颖颖与楼之间的距离
, 颖颖与楼之间的距离![]() (
(![]() ,
, ![]() ,
, ![]() 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高![]() , 亮亮蹲地观测时眼睛到地面的距离
, 亮亮蹲地观测时眼睛到地面的距离![]() . 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
. 你能根据以上测量数据帮助他们求出住宅楼的高度吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.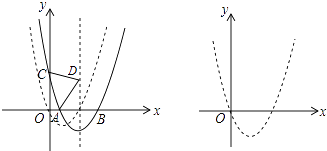
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直线y=﹣x沿y轴向下平移后的直线恰好经过点A(2,﹣4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com