
【题目】环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5[1]检测,某日随机抽取25个监测点的数据,并绘制成统计表和扇形统计图如下:
类别 | 组别 | PM2.5日平均浓度值 (微克/立方米) | 频数 | 百分比 |
A | 1 | 15≤浓度值<30 | 2 | 8% |
2 | 30≤浓度值<45 | 3 | 12% | |
B | 3 | 45≤浓度值<60 | a | b |
4 | 60≤浓度值<75 | 5 | 20% | |
C | 5 | 75≤浓度值<90 | 6 | c |
D | 6 | 90≤浓度值<105 | 4 | 16% |
合计 | 25 | 1.00 | ||
[1]“PM2.5
根据图表中提供的信息解答下列问题:
(1)统计表中的a= ,b= ,c= ;
(2)在扇形统计图中,A类所对应的圆心角是 度;
(3)我国PM2.5安全值的标准采用世卫组织(WHO)设定的最宽限值:日平均浓度小于75微克/立方米.请你估计当日环保监测中心在检测100个城市中,PM2.5日平均浓度值符合安全值的城市约有多少个?

【答案】(1)5,20%,24%;(2)72;(3)PM2.5日平均浓度值符合安全值的城市约有60天.
【解析】
(1)根据题意和表格中的数据可以求得a、b、c的值;
(2)根据表格中的数据可以得到在扇形统计图中,A类所对应的圆心角的度数;
(3)根据表格中的数据可以得到PM2.5日平均浓度值符合安全值的城市约有多少天.
(1)由题意可得,
a=25﹣(2+3+5+6+4)=25﹣20=5,b=![]() =20%,c=
=20%,c=![]() =24%,
=24%,
故答案为:5,20%,24%;
(2)在扇形统计图中,A类所对应的圆心角是:360°×(8%+12%)=72°,
故答案为:72;
(3)由题意可得,
PM2.5日平均浓度值符合安全值的城市约有:100×(8%+12%+20%+20%)=60(天),
即PM2.5日平均浓度值符合安全值的城市约有60天.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,二次函数![]() 的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:
的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:![]() 交BD于点E,连接BC的直线交直线l于K点.
交BD于点E,连接BC的直线交直线l于K点.
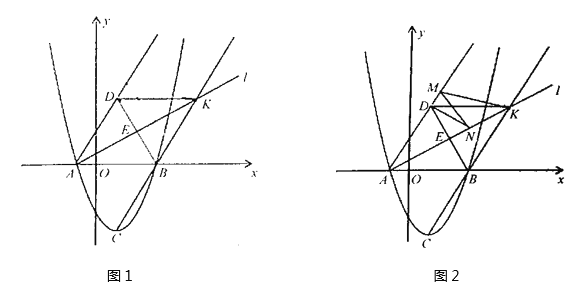
(1)问:在四边形ABKD内部是否存在点P,使它到四边形ABKD四边的距离都相等?
若存在,请求出点P的坐标;若不存在,请说明理由;
(2)若M,N分别为直线AD和直线l上的两个动点,连结DN,NM,MK,如图2,求DN+NM+MK和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴的交点为A,B.按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交AB,x轴于点C,D;②分别以点C,D为圆心,大于
与x轴、y轴的交点为A,B.按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交AB,x轴于点C,D;②分别以点C,D为圆心,大于![]() 的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交y轴于点E.则点E的坐标为( )
的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交y轴于点E.则点E的坐标为( )

A.(0,![]() )B.(0,
)B.(0,![]() )C.(0,
)C.(0,![]() )D.(0,
)D.(0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
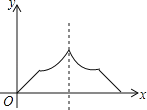
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
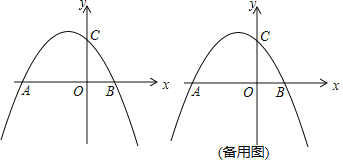
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点A、B,与y轴交于点C,点A的坐标为(-4,0),P是抛物线上一点 (点P与点A、B、C不重合).
轴交于点A、B,与y轴交于点C,点A的坐标为(-4,0),P是抛物线上一点 (点P与点A、B、C不重合).
(1)b= ,点B的坐标是 ;
(2)设直线PB直线AC交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;
(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=-3x+t上.
(1)求点C的坐标;
(2)当y1随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2-5n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
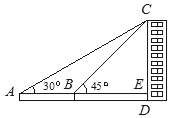
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了40m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(结果精确到1m)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com