
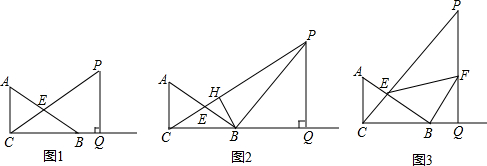
���� ��1���ɡ�ABC�ס�PCQ��$\frac{AB}{PC}=\frac{BC}{CQ}$���г����̼��ɽ����
��2���ɡ�ABC�ס�BCH��$\frac{AC}{BH}=\frac{AB}{BC}$���г����̼��ɽ����
��3�����ɡ�ABC�ס�BFQ��$\frac{AB}{BF}=\frac{AC}{BQ}$��BF=$\frac{5}{3}$��$\frac{5}{4}x-2$�������ɡ�ACB�ס�EBF��$\frac{AC}{EB}=\frac{BC}{BF}$���г����̼��ɽ����
��� �⣺��1����ͼ1�У� ��RT��ABC�У���AB=5��AC=3��
��RT��ABC����AB=5��AC=3��
��BC=$\sqrt{{5}^{2}-{3}^{2}}$=4��
��PQ��CQ��
���PQC=��ACB=90�㣬
��AE=EB��
��CE=EB=AE$\frac{5}{2}$��
��PCQ=��ABC��
���ABC�ס�PCQ��
��$\frac{AB}{PC}=\frac{BC}{CQ}$��
��$\frac{5}{\frac{5}{2}+x}=\frac{4}{4+BQ}$��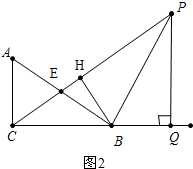
��BQ=$\frac{4}{5}x-2$��
��2����ͼ2�У���BPƽ�֡�CPQ��BH��PC��BQ��PQ��
��BH=BQ=$\frac{4}{5}x-2$��
�ߡ�ABC=��HCB����BHC=��ACB=90�㣬
���ABC�ס�BCH��
��$\frac{AC}{BH}=\frac{AB}{BC}$��
��$\frac{3}{\frac{4}{5}x-2}=\frac{5}{4}$��
��x=$\frac{11}{2}$��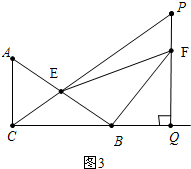
��PE=$\frac{11}{2}$��
��3����ͼ3��
�ߡ�FBQ+��ABC=90�㣬��A+��ABC=90�㣬
���A=��FBQ��
�ߡ�ACB=��EBF=90�㣬
���ABC�ס�BFQ��
��$\frac{AB}{BF}=\frac{AC}{BQ}$��
��BF=$\frac{5}{3}$��$\frac{4}{5}x-2$��=$\frac{4x-10}{3}$��
�ߡ�FEB=��A����EBF=��ACB=90�㣬
���ACB�ס�EBF��
��$\frac{AC}{EB}=\frac{BC}{BF}$��
��$\frac{3}{\frac{5}{2}}$=$\frac{4}{\frac{4x-10}{3}}$
��x=5��
���� ���⿼�����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ�����ȷѰ�����������Σ�ѧ��ת����˼�룬�÷���ȥ������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
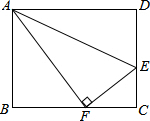 ��ͼ����E�Ǿ���ABCD�ı�CD��һ�㣬�ѡ�ADE��AE���ۣ���D�ĶԳƵ�Fǡ������BC�ϣ���֪AD=20cm��AB=16cm����ô�ۺ�AE�ij�Ϊ10$\sqrt{5}$��
��ͼ����E�Ǿ���ABCD�ı�CD��һ�㣬�ѡ�ADE��AE���ۣ���D�ĶԳƵ�Fǡ������BC�ϣ���֪AD=20cm��AB=16cm����ô�ۺ�AE�ij�Ϊ10$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�ı߳�Ϊ5��������ABCD�ĶԳ�����Ϊԭ��O��ƽ����AD��ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ����֪A��-1��2������D��˫����y=$\frac{k}{x}$�ϣ�
��ͼ������ABCD�ı߳�Ϊ5��������ABCD�ĶԳ�����Ϊԭ��O��ƽ����AD��ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ����֪A��-1��2������D��˫����y=$\frac{k}{x}$�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
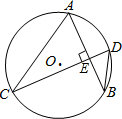 ��ͼ��AB��CD�ǡ�O�ң���AB��CD������CDB=50�㣬���ACD�Ĵ�СΪ��������
��ͼ��AB��CD�ǡ�O�ң���AB��CD������CDB=50�㣬���ACD�Ĵ�СΪ��������| A�� | 30�� | B�� | 35�� | C�� | 40�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABO�У���������A��B������ֱ�ΪA��6��6����B��8��2�����߶�CD����OΪλ�����ģ��ڵ�һ�����ڽ��߶�AB��СΪԭ����һ���õ��߶Σ���˵�D������Ϊ��������
��ͼ���ڡ�ABO�У���������A��B������ֱ�ΪA��6��6����B��8��2�����߶�CD����OΪλ�����ģ��ڵ�һ�����ڽ��߶�AB��СΪԭ����һ���õ��߶Σ���˵�D������Ϊ��������| A�� | ��3��3�� | B�� | ��4��3�� | C�� | ��3��1�� | D�� | ��4��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
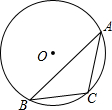 ��ͼ����ABC�ڽ��ڡ�O��BC=8����O�뾶Ϊ5����sinA��ֵΪ��������
��ͼ����ABC�ڽ��ڡ�O��BC=8����O�뾶Ϊ5����sinA��ֵΪ��������| A�� | $\frac{3}{5}$ | B�� | $\frac{4}{5}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com