
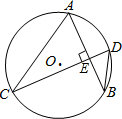
 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
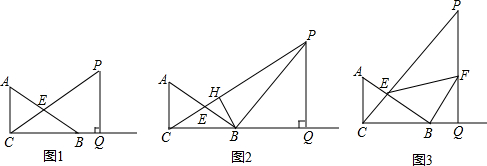
 已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )| A. | 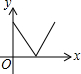 | B. | 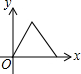 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
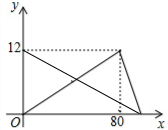 完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:
完全相同的甲、乙两个水槽,分别有一个进水管和若干个出水管,甲槽有12升水,由于工作人员马虎,他关闭进水管和出水管时,有一个出水管未关,水以每分钟0.12升的速度滴下,乙槽原来没有水,同时开放进水管和一个出水管一段时间后,关闭进水管,又打开a个出水管,存水量y(升)与时x(分)之间的函数图象如图所示,请结合图象回答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com