练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知$\sqrt{13}$的整数部分是a，小数部分是b，则2a+b的值是多少？

    分析 因为3＜$\sqrt{13}$＜4，所以$\sqrt{13}$的整数部分a=3，则小数部分b=$\sqrt{13}$-3，进一步把代数式化简，代入求值即可．

    解答 解：∵3＜$\sqrt{13}$＜4，
    ∴$\sqrt{13}$的整数部分a=3，则小数部分b=$\sqrt{13}$-3，
    ∴2a+b=6$+\sqrt{13}$-3=9$+\sqrt{13}$，
    ∴2a+b的值是3$+\sqrt{13}$．

    点评 此题考查无理数的估算方法，代数式求值等知识点，注意利用夹逼法得出a，b的值是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为3万元，可变成本逐年增长，已知该养殖户第1年的可变成本为2万元，设可变成本平均的每年增长的百分率为x．
    （1）用含x的代数式表示第3年的可变成本为2（1+x）2万元；
    （2）如果该养殖户第3年的养殖成本为5.42万元，求可变成本平均每年增长的百分率；
    （3）若可变成本平均每年的增长的百分率保持不变，通过计算，判断该养殖户第5年的养殖成本会不会超过6万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，在笔直的公路L的同侧有A、B两个村庄，已知A、B两村分别到公路的距离AC=3km，BD=4km．现要在公路上建一个汽车站P，使该车站到A、B两村的距离相等，
    （1）试用直尺和圆规在图中作出点P；（保留作图痕迹）
    （2）若连接AP、BP，测得∠APB=90°，求A村到车站的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知二元一次方程组$\left\{\begin{array}{l}5x+8y=18\\ 3x-y=7\end{array}$，则8x+7y=25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．△ABC是等边三角形，点D、E分别在边AB、BC上，CD、AE交于点F，∠AFD=60°．
    （1）如图1，求证：BD=CE；
    （2）如图2，FG为△AFC的角平分线，点H在FG的延长线上，HG=CD，连接HA、HC，求证：∠AHC=60°；
    （3）在（2）的条件下，若AD=2BD，FH=9，求AF长．

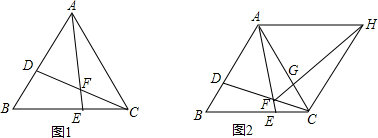
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，已知点P在△ABC的边AC上，下列条件中，不能判断△ABP∽△ACB的是（　　）
    A．∠ABP=∠CB．∠APB=∠ABCC．AB2=AP•ACD．$\frac{AB}{BP}$=$\frac{AC}{CB}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．点M为数轴上表示-2的点，将点M沿数轴向右平移5个单位到点N，则点N表示的数是（　　）
    A．3B．5C．-7D．3或-7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标有的三个数值为-5，-1，3．乙袋中的三张卡片所标的数值为-3，2，7．先从甲袋中随机取出一张卡片，用a表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用b表示取出卡片上的数值，把a、b分别作为点A的横坐标和纵坐标．
    （1）请用列表或画树状图的方法写出带你A（a，b）的所有情况．
    （2）求点A落在第二象限的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，AB、CD是⊙O弦，且AB⊥CD，若∠CDB=50°，则∠ACD的大小为（　　）
    A．30°B．35°C．40°D．50°

    查看答案和解析>>

    同步练习册答案