
 如图,在笔直的公路L的同侧有A、B两个村庄,已知A、B两村分别到公路的距离AC=3km,BD=4km.现要在公路上建一个汽车站P,使该车站到A、B两村的距离相等,
如图,在笔直的公路L的同侧有A、B两个村庄,已知A、B两村分别到公路的距离AC=3km,BD=4km.现要在公路上建一个汽车站P,使该车站到A、B两村的距离相等,分析 (1)连接AB,作AB的垂直平分线与AB交于点P即可;
(2)先利用AAS证明△ACP≌△PDB,得出CP=BD=4km,然后在Rt△ACP中利用勾股定理求出AP2=AC2+CP2=32+42=25,则AP=5.
解答 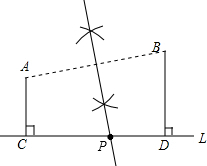 解:(1)连结AB,画出AB的垂直平分线交CD于P,
解:(1)连结AB,画出AB的垂直平分线交CD于P,
则点P即为所求的点;
(2)∵∠APB=90°,
∴∠APC+∠BPD=90°,
又∵∠APC+∠CAP=90°,
∴∠CAP=∠BPD,
又∵∠ACP=∠PDB=90°,
∵MN垂直平分AB,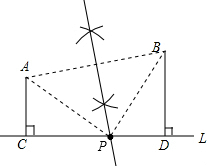 ∴AP=BP,
∴AP=BP,
∴△ACP≌△PDB(AAS),
∴CP=BD=4km,
在Rt△ACP中,∠ACP=90°,
AP2=AC2+CP2=32+42=25,
∴AP=5.
答:A村到车站的距离5km.
点评 本题考查了勾股定理的应用,线段垂直平分线的判定,全等三角形的判定与性质,作线段的垂直平分线,作出点P是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
 九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了10米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).求旗杆AB的高度(精确到0.1米,已知$\sqrt{3}$≈1.73).
九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了10米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).求旗杆AB的高度(精确到0.1米,已知$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y2<y3<y1 | D. | y1<y2<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.
已知:如图,在?ABCD中,点E在BC边上,连接AE,O为AE中点,连接BO并延长交AD于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com