Question

4．△ABC是等边三角形，点D、E分别在边AB、BC上，CD、AE交于点F，∠AFD=60°．
（1）如图1，求证：BD=CE；
（2）如图2，FG为△AFC的角平分线，点H在FG的延长线上，HG=CD，连接HA、HC，求证：∠AHC=60°；
（3）在（2）的条件下，若AD=2BD，FH=9，求AF长．

Answer 1

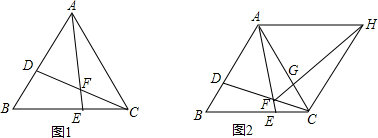
分析 （1）根据等边三角形的性质得出AB=BC，∠BAC=∠C=∠ABE=60°，根据SAS推出△ABE≌△BCD，即可证得结论；
（2）根据角平分线的性质定理证得CM=CN，利用∠CEM=∠ACE+∠CAE=60°+∠CAE，∠CGN=∠AFH+∠CAE=60°+∠CAE，得出∠CEM=∠CGN，然后根据AAS证得△ECM≌△GCN，得出CG=CE，EM=GN，∠ECM=∠GCN，进而证得△AMC≌△HNC，得出∠ACM=∠HCN，AC=HC，从而证得△ACH是等边三角形，证得∠AHC=60°；
（3）在FH上截取FK=FC，得出△FCK是等边三角形，进一步得出FC=KC=FK，∠ACF=∠HCK，证得△AFC≌△HKC得出AF=HK，从而得到HF=AF+FC=9，由AD=2BD可知AG=2CG，再由$\frac{{S}_{△AEG}}{{S}_{△CFG}}$=$\frac{AG}{GC}$，根据等高三角形面积比等于底的比得出$\frac{{S}_{△AEG}}{{S}_{△CFG}}$=$\frac{\frac{1}{2}AF•GW}{\frac{1}{2}CF•GQ}$=$\frac{AF}{CF}$=2，再由AF+FC=9求得．

解答 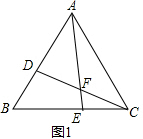解：（1）如图1，∵△ABC是等边三角形，
∴∠B=∠ACE=60°BC=AC，
∵∠AFD=∠CAE+∠ACD=60°∠BCD+∠ACD=∠ACB=60°，
∴∠BCD=∠CAE，
在△ABE和△BCD中，
$\left\{\begin{array}{l}{∠B=∠ACE}\\{BC=AC}\\{∠BCD=∠CAE}\end{array}\right.$
∴△ABE≌△BCD（ASA），
∴BD=CE；
（2）如图2，作CM⊥AE交AE的延长线于M，作CN⊥HF于N，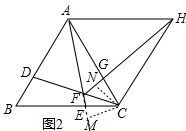
∵∠EFC=∠AFD=60°
∴∠AFC=120°，
∵FG为△AFC的角平分线，
∴∠CFH=∠AFH=60°，
∴∠CFH=∠CFE=60°，
∵CM⊥AE，CN⊥HF，
∴CM=CN，
∵∠CEM=∠ACE+∠CAE=60°+∠CAE，∠CGN=∠AFH+∠CAE=60°+∠CAE，
∴∠CEM=∠CGN，
在△ECM和△GCN中
$\left\{\begin{array}{l}{∠CEM=∠CGN}\\{∠CME=∠CNG=90°}\\{CM=CN}\end{array}\right.$
∴△ECM≌△GCN（AAS），
∴CE=CG，EM=GN，∠ECM=∠GCN，
∴∠MCN=∠ECG=60°，
∵△ABE≌△BCD，
∵AE=CD，
∵HG=CD，
∴AE=HG，
∴AE+EM=HG+GN，即AM=HN，
在△AMC和△HNC中
$\left\{\begin{array}{l}{AM=HN}\\{∠AMC=∠HNC=90°}\\{CM=CN}\end{array}\right.$
∴△AMC≌△HNC（SAS），
∴∠ACM=∠HCN，AC=HC，
∴∠ACM-∠ECM=∠HCN-∠GCN，即∠ACE=∠HCG=60°，
∴△ACH是等边三角形，
∴∠AHC=60°；
（3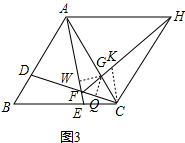）如图3，在FH上截取FK=FC，
∵∠HFC=60°，
∴△FCK是等边三角形，
∴∠FKC=60°，FC=KC=FK，
∵∠ACH=60°，
∴∠ACF=∠HCK，
在△AFC和△HKC中
$\left\{\begin{array}{l}{FC=KC}\\{∠ACF=∠HCK}\\{AC=HC}\end{array}\right.$
∴△AFC≌△HKC（SAS），
∴AF=HK，
∴HF=AF+FC=9，
∵AD=2BD，BD=CE=CG，AB=AC，
∴AG=2CG，
∴$\frac{{S}_{△AFG}}{{S}_{△CFG}}$=$\frac{AG}{GC}$=$\frac{2}{1}$，
作GW⊥AE于W，GQ⊥DC于Q，
∵FG为△AFC的角平分线，
∴GW=GQ，
∵$\frac{{S}_{△AFG}}{{S}_{△CFG}}$=$\frac{\frac{1}{2}AF•GW}{\frac{1}{2}CF•GQ}$=$\frac{AF}{CF}$=$\frac{2}{1}$，
∴AF=2CF，
∴AF=6．

点评 本题考查了全等三角形的判定和性质，等边三角形的判定和性质，角平分线的性质，找出辅助线根据全等三角形和等边三角形是解题的关键．