
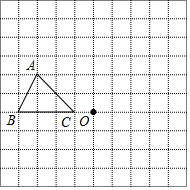
 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).分析 (1)关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分,据此进行作图即可;
(2)通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形;根据线段BC扫过的面积=S扇形BOB2-S扇形COC2,进行计算即可.
解答 解:(1)如图所示,△A1B1C1即为所求;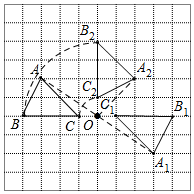
(2)如图所示,△A2B2C2即为所求;
线段BC扫过的面积=S扇形BOB2-S扇形COC2,
=$\frac{90•π•{4}^{2}}{360}$-$\frac{90•π•{1}^{2}}{360}$
=$\frac{15}{4}π$.
点评 本题主要考查了利用旋转变换进行作图以及扇形面积的计算,解决问题时注意:旋转作图有自己独特的特点,决定图形位置的因素有旋转角度、旋转方向、旋转中心,任意不同,位置就不同,但得到的图形全等.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com