
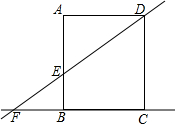
 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6. 分析 分两种情况讨论:若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,求出即可.
解答 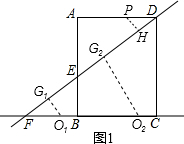 解:∵AD∥BC,
解:∵AD∥BC,
∴△EBF∽△EAD,
∴$\frac{EF}{10}$=$\frac{3}{6}$=$\frac{BF}{8}$,
∴EF=5,BF=4,
如图1,若⊙O1与直线DE、AB都相切,且圆心O1在AB的左侧,过点O1作O1G1⊥DF于G1,
则可设O1G1=O1B=r1,
∵S△EO1F+S△EBO1=S△EBF,
∴$\frac{1}{2}$r1×5+$\frac{1}{2}$r1×3=$\frac{1}{2}$×3×4,
解得:r1=$\frac{3}{2}$,
若⊙O2与直线DE、AB都相切,且圆心O2在AB的右侧,过点O2作O2G2⊥DF于G2,
则可设O2G2=O2B=r2,
∵S△FO2D=$\frac{1}{2}$FO2×DC=$\frac{1}{2}$DF×O2G2,
∴$\frac{1}{2}$×(4+r2)×(6+3)=$\frac{1}{2}$×(10+5)×r2,
解得:r2=6,
即满足条件的圆的半径为$\frac{3}{2}$或6;
故答案为:$\frac{3}{2}$或6.
点评 此题主要考查了圆的综合应用以及切线的性质以及相似三角形的判定与性质等知识,利用分类讨论得出是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
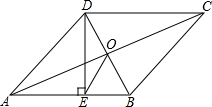 如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )
如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
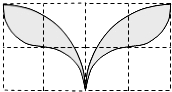 如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为的正方形,则以格点为圆心,半径为和2的两种弧围成的“叶状”阴影图案的面积为( )| A. | 4π-2 | B. | 2π-2 | C. | 4π-4 | D. | 2π-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
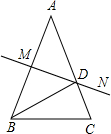 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )| A. | 0 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com