
����Ŀ��ij�泡�ƻ�����ס����������繲6000β����������ÿβ0.5Ԫ����������ÿβ0.8Ԫ��������ϱ������ס�����������ijɻ��ʷֱ�Ϊ90%��95%��
��1���������������繲����3600Ԫ����ס�����������������˶���β��
��2�����������������Ǯ������4200Ԫ��Ӧ���ѡ�����磿
��3����Ҫʹ��������ijɻ��ʲ�����93%���ҹ���������ܷ�����ͣ�Ӧ���ѡ�����磿
���𰸡���1������������4000β������������2000β����2�������������Ӧ������2000β����3�������������2400β����������3600βʱ���ܷ������.
��������
�⣺��1���蹺���������xβ��������������![]() β��
�
������ã�![]()
��ã�![]()
��![]()
�𣺼���������4000β������������2000β��
��2��������ã�![]()
��ã�![]()
�������������Ӧ������2000β��
��3���蹺��������ܷ���Ϊy����![]()
�����⣬��![]()
��ã�![]()
��![]() ��
��
��![]() ��
��
��y��x�����������
�൱![]() ʱ��
ʱ��![]() ��
��
�������������2400β����������3600βʱ���ܷ�����ͣ�


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
������![]() ��
��![]() ����ͼ��
����ͼ��![]() ������
������![]() ��4��1����ֱ��
��4��1����ֱ��![]() ��ͼ��
��ͼ��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2���ᡢ�����궼�������ĵ�������㣮��ͼ��![]() �ڵ�
�ڵ�![]() ��
��![]() ֮��IJ������߶�
֮��IJ������߶�![]() ��
��![]() ��
��![]() Χ�ɵ��������߽磩Ϊ
Χ�ɵ��������߽磩Ϊ![]() ��
��
�ٵ�![]() ʱ��ֱ��д������
ʱ��ֱ��д������![]() �ڵ����������
�ڵ����������
��������![]() ��ǡ��4�����㣬��Ϻ���ͼ����
��ǡ��4�����㣬��Ϻ���ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
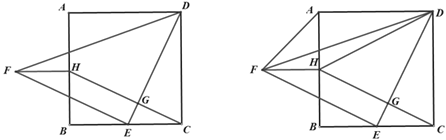
����Ŀ����֪����������ABCD�У���E�� BC���ϣ����� DE����DEΪֱ�DZ�������ֱ��������EDF����DEF=90����������C�� DE�Ĵ��ߣ�����ΪG����AB�ڵ�H������ FH��
��1����ͼ 1����֤���ı���FECHΪƽ���ı���
��2����ͼ 2������ DH�� AF���� E Ϊ BC �е㣬�ڲ������κθ���������ĸ������£���ֱ��д����ƽ���ı���FECH�����ȵ����������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ϸ������һ��С��С������ֱƽ���ڵ�A��C��������ذڶ���A����������AN=14cm��С������͵�Bʱ����������BM=5cm����AOB=66������ϸ��OB�ij��ȣ����ο����ݣ�sin66���0.91��cos66���0.40��tan66���2.25��
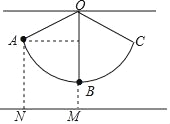
���𰸡�15cm
��������
������ϸ��OB�ij���Ϊxcm����AD��OB��D��֤���ı���ANMD�Ǿ��Σ��ó�AN=DM=14cm�����OD=x-9����Rt��AOD�У������Ǻ����ó����̣��ⷽ�̼��ɣ�
�����������ϸ��OB�ij���Ϊxcm����AD��OB��D����ͼ��ʾ��
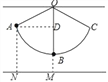
���ADM=90�㣬
�ߡ�ANM=��DMN=90�㣬
���ı���ANMD�Ǿ��Σ�
��AN=DM=14cm��
��DB=14��5=9cm��
��OD=x��9��
��Rt��AOD��cos��AOD=![]() ��
��
��cos66��=![]() =0.40��
=0.40��
��ã�x=15��
��OB=15cm��
�����͡������
��������
20
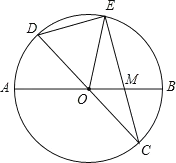
����Ŀ����֪����ͼ���ڰ뾶Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ����
������ֱ����![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() ����
����![]() ������
������![]() ��
��![]() .
.
��1����֤��![]() ;
;
��2����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ�����������֡������������������ĸ����Ŀ�������ȡ����ѧ������ѡ��μӵĻ��Ŀ���е���ͳ�ƣ��Ƴ���������������ͳ��ͼ��
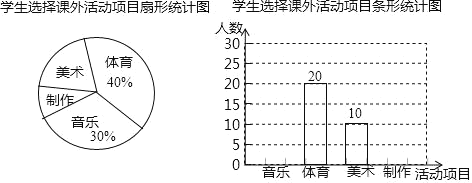
���������ͳ��ͼ�ṩ����Ϣ������������⣺
��1����������������������
��2���벹ȫ��������ͳ��ͼ�����������ͼ�С���������ռ��Բ�ĽǶ�����
��3������У��2000��ѧ���������ô��������Ʋμӡ�����������Ŀ���������������������֡��͡�������������Ŀ����ѧ������ԼΪ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
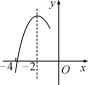
����Ŀ����ͼ��������y��ax2��bx��c��a��0���ĶԳ���Ϊֱ��x����2����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���4a��b��0����c<0���ۣ�3a��c>0����4a��2b>at2��bt��tΪʵ�������ݵ�![]() ��
��![]() ��
��![]() �Ǹ��������ϵĵ㣬��y1<y2<y3��������ȷ���۵ĸ����ǣ�������
�Ǹ��������ϵĵ㣬��y1<y2<y3��������ȷ���۵ĸ����ǣ�������
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
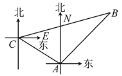
����Ŀ����ͼ���ס���ֻ���̴�ͬʱ��A�۳������㣬�״���ÿСʱ15![]() km���ٶ��ر�ƫ��60�㷽��ǰ�����Ҵ���ÿСʱ15 km���ٶ��ض�������ǰ�����״�����2 h����C������ʱ�״�������߶������Ҵ��ϣ����Ǽ״�����(����)�ر�ƫ��75��ķ������Ҵ������������B���������ʣ�
km���ٶ��ر�ƫ��60�㷽��ǰ�����Ҵ���ÿСʱ15 km���ٶ��ض�������ǰ�����״�����2 h����C������ʱ�״�������߶������Ҵ��ϣ����Ǽ״�����(����)�ر�ƫ��75��ķ������Ҵ������������B���������ʣ�
(1)�״���C�����������Ҵ����˶���ʱ�䣿
(2)�״����Ҵ����ٶ���ÿСʱ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����70���꣬ijУ���а༶��ӽ�����������У����Ұ��㣬�й��������質����������Һ��ҵ���������ֱ�����ĸA��B��C���α�ʾ����������������ʱ����A��B��C��������ĸ�ֱ�д��3��������Ŀ�Ƭ�����ϣ�ϴ�Ⱥ��������·��������ϣ��ˣ�1�����ȴ��������ȡһ�ſ�Ƭ���Żغ�ϴ�ȣ����ɰˣ�2�������������ȡһ�ſ�Ƭ�����и�ӽ������
��1���ˣ�1������и������Һ��ҵ�������ĸ�����__________��
��2�����û���״ͼ���б��ķ�����ʾ���п��ܵĽ����������ˣ�1����Ͱˣ�2������в�ͬ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com