
����Ŀ����֪�����߾�����A����3��0����F��8��0����B��0��4������
��1���������߽���ʽ���Գ��
��2������D���߶�FB���˶�������F��B�غϣ�������D��DC�����ڵ�C��x��0��������FCD��CD�����ۣ���B��Ӧ��Ϊ��E����CDE���FBO�ص��������ΪS��
�������S��x֮��ĺ�����ϵʽ����д���Ա���ȡֵ��Χ��
���Ƿ���������ĵ�C��ʹ�á�BDEΪֱ�������Σ������ڣ����C�����꣬�������ڣ���˵�����ɣ�
��3�������߶Գ�������һ��M��ƽ������һ��N������A��B��M��N�ĵ���ɵ��ı���Ϊ���Σ����N�����꣮
���𰸡�
��1��
�⣺�������߽���ʽΪy=a��x+3����x��8����
����B��0��4�������4=a����0+3������0��8����
���a=�� ![]() ��
��
�������߽���ʽΪy=�� ![]() ��x+3����x��8����
��x+3����x��8����
�Գ���Ϊx=����3+8����2= ![]() ��
��
��2��
�⣺CE=CF=8��x��CD=4�� ![]() x��
x��
�ٵ�0��x��4ʱ��
S= ![]() ��8��x����4��
��8��x����4�� ![]() x����[1����
x����[1���� ![]() ��2]=��
��2]=�� ![]() x2+4x��
x2+4x��
��4��x��8ʱ��
S= ![]() ��8��x����4��
��8��x����4�� ![]() x��=
x��= ![]() x2��4x+16��
x2��4x+16��
�ڷ��������������BED=90��ʱ����BOE�ס�ECD��
�� ![]() =
= ![]() =2��
=2��
��EC=3��
��C1��5��0����
����EBD=90��ʱ��
��EOB�ס�BOF��
�� ![]() =
= ![]() =2��
=2��
��EO=2��
��EC= ![]() =5��
=5��
��C2��3��0����
��3��
�⣺����ABΪ�ߣ���BΪԲ�ģ�ABΪ�뾶��Բ���Գ�����M1��M2���㣬
M1I= ![]() =
= ![]() ��
��
��BM1��ƽ����AN1�ã�N1���� ![]() ��
�� ![]() ����N2����
����N2���� ![]() ����
���� ![]() ����
����
��AΪԲ�ģ�ABΪ�뾶��Բ����ʱ��Գ���û�н��㣬�ʲ����ڣ�
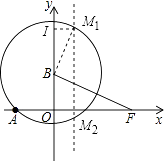
����ABΪ�Խ��ߣ�ֱ��AB�Ľ���ʽΪ��y= ![]() x+4��
x+4��
��AB���д���MN�Ľ���ʽΪ��y=�� ![]() x+
x+ ![]() ��
��
��x= ![]() ʱ��y=��1��
ʱ��y=��1��
��M�� ![]() ����1����
����1����
��N3���� ![]() ��5����
��5����
����������N1���� ![]() ��
�� ![]() ����N2����
����N2���� ![]() ����
���� ![]() ����N3����
����N3���� ![]() ��5����
��5����
����������1�����������߽���ʽΪy=a��x+3����x��8��������B��0��4��������֪�����߷��̣����a��ֵ���ɣ���2���ٷ����������0��x��4��4��x��8���������ۿ���S��x֮��ĺ�����ϵʽ���ڷ��������������BED=90��ʱ������EBD=90��ʱ���������ۿ���C�����ꣻ��3�����������������ABΪ�ߣ���BΪԲ�ģ�ABΪ�뾶��Բ���Գ�����M1 �� M2���㣻����ABΪ�Խ��ߣ��������ۿ����N�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ϳ�����30����Ա���±��Ǻϳ��ų�Ա������ֲ�ͳ�Ʊ���
���䣨��λ���꣩ | 13 | 14 | 15 | 16 |
Ƶ������λ������ | 5 | 15 | x | 10��x |
���ڲ�ͬ��x�����й��������ͳ�������ᷢ���ı���ǣ� ��
A.ƽ��������λ��
B.ƽ����������
C.���������
D.����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijְҵ���л�����ѧ��42�ˣ���������������Ů��������2����3�ˣ�
��1���ð�������Ů�����ж����ˣ�
��2��ij�����������ð���¼30��ѧ���������ԣ��ð��С�Ů��ÿ���ܼӹ���������ֱ�Ϊ50����45����Ϊ��֤����ÿ��ӹ����������������1460������ô����Ҫ��¼��������ѧ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ִ���ÿСʱ20ǧ���ٶȴӼ�ʻ��160ǧ��Զ���Ҹۣ�2Сʱ��һ�ҿ�ͧ��ÿСʱ40ǧ���ٶ�Ҳ�Ӽ�ʻ���Ҹ����ֱ��г��ִ��Ϳ�ͧ��ʻ��·��y��ǧ�ף���ʱ��x��Сʱ���ĺ�����ϵʽ������ͼ�е�ֱ������ϵ�л�������ͼ�۲�ͼ��ش��������⣺
��1����ʱ�ִ���ʻ�ڿ�ͧ��ǰ�棿
��2����ʱ��ͧ��ʻ���ִ���ǰ�棿
��3����һ�Ҵ���ʻ��60ǧ�ף���һ�Ҵ���ʻ��100ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a+b��3��ab��1��
��1��a2+b2��
��2����a��b��2��
��3��ab3+a3b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ȼ��Ч������ָ����ÿ����1��������ʻ�������. ��ȼ��Ч����Խ�߱�ʾ����ÿ����1��������ʻ�������Խ�ࣻ��ȼ��Ч����Խ�ͱ�ʾ����ÿ����1��������ʻ�������Խ��. ��ͼ�����˼ס��ҡ������������ڲ�ͬ�ٶ��µ�ȼ��Ч�����.
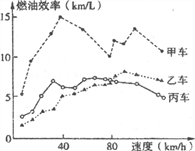
����ͼ���ṩ����Ϣ������˵����
������ͬ�ٶ���ʻ��ͬ·�̣��������У��׳������������
���Ե���80km/h���ٶ���ʻʱ����ʻ��ͬ·�̣��������У��ҳ�������������
���Ը���80km/h���ٶ���ʻʱ����ʻ��ͬ·�̣��ҳ��ȱ���ʡ��
����80km/h���ٶ���ʻʱ����ʻ100����׳����ĵ�������ԼΪ10��
��ȷ����________����д��ȷ���۵���ţ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ͷ��13800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼۣ�Ԫ/�䣩 |
�� | 24 | 36 |
�� | 33 | 48 |
��1�����̳������ס������ֿ�Ȫˮ�������䣿
��2��ȫ������500���Ȫˮ�����̳�������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x + 2��0 = 1���� ��
A.x = 3B.x = 1C.xΪ����ʵ��D.x ��- 2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com