
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
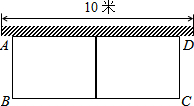 如图所示,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的矩形花圃,如果花圃的面积为42平方米,求花圃的宽AB.
如图所示,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的矩形花圃,如果花圃的面积为42平方米,求花圃的宽AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
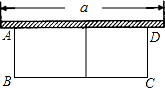 如图所示某农户打算建造一个花圃种植两种不同的花卉供应城市市场,这是需要用长为24米的篱笆靠着墙(墙的最大可用长度为a是10米),围成中间隔有道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.
如图所示某农户打算建造一个花圃种植两种不同的花卉供应城市市场,这是需要用长为24米的篱笆靠着墙(墙的最大可用长度为a是10米),围成中间隔有道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+3x-2=0 | B. | x2+3x+2=0 | C. | x2-3x+2=0 | D. | x2-3x-2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,所给的图案由△ABC绕点O顺时针旋转( )前后的图形组成的.
如图,所给的图案由△ABC绕点O顺时针旋转( )前后的图形组成的.| A. | 45°、90°、135° | B. | 90°、135°、180° | ||
| C. | 45°、90°、135°、180°、225° | D. | 45°、135°、225°、270° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com