
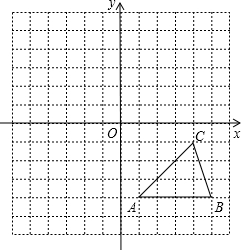
 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(4,-1).
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(4,-1).分析 (1)过A作y轴垂线,截取DA1=DA,B1D=BD,过C作y轴垂线,截取C1E=CE,连接A1B1,A1C1,B1C1,△A1B1C1为所求三角形,写出点C1的坐标即可;
(2)连接OA1,OB1,OC1,取OA1中点A2,取OB1中点B2,取OC1中点C2,连接A2B2,A2C2,B2C2,△A2B2C2为所求三角形.
解答 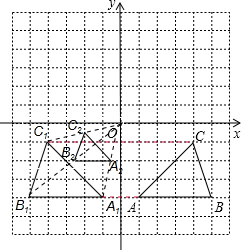 解:(1)画出△ABC以y轴为对称轴的对称图形△A1B1C1,如图所示,
解:(1)画出△ABC以y轴为对称轴的对称图形△A1B1C1,如图所示,
根据题意得:点C1的坐标为(-4,-1);
(2)以原点O为位似中心,画出△A1B1C1缩小一半后的△A2B2C2,如图所示.
点评 此题考查了作图-位似变换,作图-轴对称变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:填空题
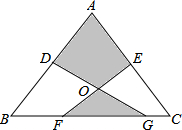 如图,在△ABC中,AB=AC=5,BC=6,D、E分别是AB、AC的中点,F、G为BC上的两点,且FG=3,线段DG、EF的交点为O,当线段FG在线段BC上移动时,△FGO的面积与四边形ADOE的面积之和恒为定值,则这个定值是6.
如图,在△ABC中,AB=AC=5,BC=6,D、E分别是AB、AC的中点,F、G为BC上的两点,且FG=3,线段DG、EF的交点为O,当线段FG在线段BC上移动时,△FGO的面积与四边形ADOE的面积之和恒为定值,则这个定值是6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
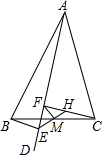 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )| A. | M是BC的中点 | B. | FM=$\frac{1}{2}$EH | C. | CF⊥AD | D. | FM⊥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
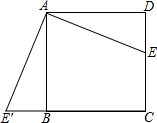 如图,在正方形ABCD中,点E为CD中点,把△ADE绕点A顺时针旋转90°,得到△ABE′,AE′=$\sqrt{5}$,则四边形AECE′的面积为4.
如图,在正方形ABCD中,点E为CD中点,把△ADE绕点A顺时针旋转90°,得到△ABE′,AE′=$\sqrt{5}$,则四边形AECE′的面积为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com