
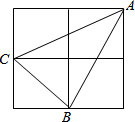
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则BC边上的高是( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{5}}{10}$ | C. | $\frac{3\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
分析 首先求出S△ACB的值,再利用勾股定理得出BC的长,再结合三角形面积求出答案.
解答 解:如图所示:S△ACB=4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×1-$\frac{1}{2}$×1×2=$\frac{3}{2}$,
设BC边上的高是h,则$\frac{1}{2}$BC•h=$\frac{3}{2}$,
∵BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴$\frac{1}{2}$×$\sqrt{2}$h=$\frac{3}{2}$,
解得:h=$\frac{3\sqrt{2}}{2}$.
故选:A.
点评 此题主要考查了勾股定理以及三角形面积求法,正确得出△ABC的面积是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.8 | B. | 6.6 | C. | 6.8 | D. | 7.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
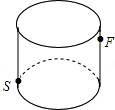 如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm,点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.
如图所示,圆柱形玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm,点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com