
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。

【答案】(1)证明见解析(2)位置关系是AD⊥GA,利用见解析.
【解析】
试题分析:(1)先根据条件证明△BHF∽△CHE得出∠ABD=∠ACG,然后可证△ABD≌△GCA,从而可得AD=AG;(2)根据△ABD≌△GCA得出∠ADB=∠GAC,然后利用角的关系得出∠AED=∠GAD=90°,即可得证.
试题解析:(1)∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,又∠BHF=∠CHE,
∴△BHF∽△CHE,
∴∠ABD=∠ACG,
在△ABD和△GCA中
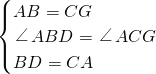 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等);
(2)位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
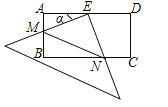
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=![]() .
.
上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把8a3-8a2+2a进行因式分解,结果正确的是( )
A.2a(4a2-4a+1)
B.8a2(a-1)
C.2a(2a-1)2
D.2a(2a+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为( )
A.(﹣3,﹣7)
B.(﹣7,﹣3)
C.(3,7)
D.(7,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD各顶点的坐标分别为A(0,1),B(5,1),C(7,3),D(2,5).
(1)在平面直角坐标系中画出该四边形;
(2)四边形ABCD内(边界点除外)一共有________个整点(即横坐标和纵坐标都是整数的点);
(3)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律下去,记∠A2B1 B2=θ1,∠A3B2B3=θ2,…,∠An+1Bn Bn+1=θn,则θ2016﹣θ2015的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图1,在数轴上A点衰示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB﹣b﹣a.
请用上面的知识解答下面的问题:
如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm.
(1)请你在数轴上表示出A.B.C三点的位置:
(2)点C到点人的距离CA= cm;若数轴上有一点D,且AD=4,则点D表示的数为 ;
(3)若将点A向右移动xcm,则移动后的点表示的数为 ;(用代数式表示)
(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,
试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com