
����Ŀ����ͼ1��������C1��y=ax2��2ax+c��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C����֪��A������Ϊ����1��0������OΪ����ԭ�㣬OC=3OA��������C1�Ķ���ΪG��
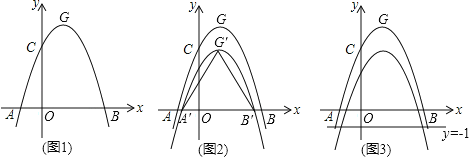
��1�����������C1�Ľ���ʽ����д����G�����ꣻ
��2����ͼ2����������C1����ƽ��k��k��0������λ���õ�������C2����C2��x��Ľ���ΪA�䡢B�䣬����ΪG�䣬����A��B��G���ǵȱ�������ʱ����k��ֵ��
��3���ڣ�2���������£���ͼ3�����MΪx����������һ���㣬����M��x��Ĵ��߷ֱ�������C1��C2��P��Q���㣬��̽����ֱ��y=��1���Ƿ���ڵ�N��ʹ����P��Q��NΪ���������������AOQȫ�ȣ������ڣ�ֱ��д����M��N�����꣺�������ڣ���˵�����ɣ�
���𰸡���1��������C1�Ľ���ʽΪy=��x2+2x+3����G������Ϊ��1��4������2��k=1����3��M1��![]() ��0����N1��
��0����N1��![]() ����1����M2��
����1����M2��![]() ��0����N2��1����1����M3��4��0����N3��10����1����M4��4��0����N4����2����1����
��0����N2��1����1����M3��4��0����N3��10����1����M4��4��0����N4����2����1����
��������
��1���ɵ�A�����꼰OC=3OA�õ�C���꣬��A��C����������ʽ���ɵã�
��2����������C2�Ľ���ʽΪy=��x2+2x+3��k����y=����x��1��2+4��k������G��D��x���ڵ�D����BD��=m���ɵȱ�����������֪��B��������Ϊ��m+1��0������G��������Ϊ��1��![]() m���������������ʽ���ɵã�
m���������������ʽ���ɵã�
��3����M��x��0������P��x����x2+2x+3����Q��x����x2+2x+2��������PQ=OA=1�ҡ�AOQ����PQN��Ϊ�۽�֪��AOQ�ա�PQN���ӳ�PQ��ֱ��y=��1�ڵ�H��֤��OQM�ա�QNH�����ݶ�Ӧ����Ƚ�������x�ķ��̣���֮���x��ֵ�Ӷ���һ����⼴����
��1���ߵ�A������Ϊ����1��0����
��OA=1��
��OC=3OA��
���C��������0��3����
��A��C�������y=ax2��2ax+c���ã�![]() ��
��
��ã�![]() ��
��
��������C1�Ľ���ʽΪy=��x2+2x+3=����x��1��2+4��
���Ե�G������Ϊ��1��4����
��2����������C2�Ľ���ʽΪy=��x2+2x+3��k����y=����x��1��2+4��k��
����G����G��D��x���ڵ�D����BD��=m��

�ߡ�A��B��G��Ϊ�ȱ������Σ�
��G��D=![]() B��D=
B��D=![]() m��
m��
���B����������m+1��0������G����������1��![]() m����
m����
����B�䡢G�����������y=����x��1��2+4��k���ã�
![]() ��
��
��ã�![]() ���ᣩ��
���ᣩ�� ��
��
��k=1��
��3����M��x��0������P��x����x2+2x+3����Q��x����x2+2x+2����
��PQ=OA=1��
�ߡ�AOQ����PQN��Ϊ�۽ǣ�
���AOQ�ա�PQN��
��ͼ2���ӳ�PQ��ֱ��y=��1�ڵ�H��

���QHN=��OMQ=90�㣬
�֡ߡ�AOQ�ա�PQN��
��OQ=QN����AOQ=��PQN��
���MOQ=��HQN��
���OQM�ա�QNH��AAS����
��OM=QH����x=��x2+2x+2+1��
��ã�x=![]() ����ֵ��ȥ����
����ֵ��ȥ����
��x=![]() ʱ��HN=QM=��x2+2x+2=
ʱ��HN=QM=��x2+2x+2=![]() ����M��
����M��![]() ��0����
��0����
���N������![]() +
+![]() ����1��������
����1��������![]() ����1����
����1����
��![]() ��
��![]() ����1��������1����1����
����1��������1����1����
��ͼ3��

ͬ���ɵ���OQM�ա�PNH��
��OM=PH����x=������x2+2x+2����1��
��ã�x=��1���ᣩ��x=4��
��x=4ʱ����M������Ϊ��4��0����HN=QM=������x2+2x+2��=6��
���N��������4+6����1������10����1������4��6����1��������2����1����
���ϵ�M1��![]() ��0����N1��
��0����N1��![]() ����1����M2��
����1����M2��![]() ��0����N2��1����1����M3��4��0����N3��10����1����M4��4��0����N4����2����1����
��0����N2��1����1����M3��4��0����N3��10����1����M4��4��0����N4����2����1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
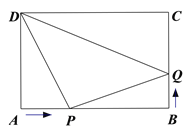
����Ŀ����ͼ���ھ���ABCD�У�AB=10cm,AD=8cm,��P�ӵ�A������AB��2cm/s���ٶ�����յ�B�˶���ͬʱ��Q�ӵ�B������BC��1cm/s���ٶ�����յ�C�˶������ǵ����յ��ֹͣ�˶�.
(1)�����P��D�ľ����ǵ�P��Q�ľ����2����
(2)�����DPQ�������24cm2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
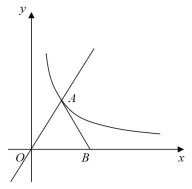
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬����������![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ������A��2��m����
��ͼ������A��2��m����
(1)���������Ľ���ʽ��
(2)��B��![]() ����ϣ���OA=BA������������ͼ������һ��C���ҡ�ABC=90�������C���꣮
����ϣ���OA=BA������������ͼ������һ��C���ҡ�ABC=90�������C���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y��kx+k+1��ͼ����һ�κ���y����x+4��ͼ���ڵ�A��1��a����

��1����a��k��ֵ��
��2������ͼ��д������ʽ��x+4��kx+k+1�Ľ⣻
��3�����ͼ�Σ���x��2ʱ����һ�κ���y����x+4����ֵy��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˹��������Լ��ˮ������ʵ�������շ��ƣ���ÿ����ˮ��������12������12����ʱ��ÿ�ְ����������Żݼ��շѣ�ÿ�³���12�֣���������ÿ�ְ��г����ڼ��շѣ�С�Ƽ�1�·���ˮ24�֣���ˮ��42Ԫ��2�·���ˮ20�֣���ˮ��32Ԫ��
��1����ÿ��ˮ�����������Żݼۺ��г����ڼ۷ֱ��Ƕ���Ԫ��
��2����ÿ����ˮ��Ϊ![]() �֣�Ӧ��ˮ��Ϊ
�֣�Ӧ��ˮ��Ϊ![]() Ԫ��д��
Ԫ��д��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3��С�Ƽ�3�·���ˮ26�֣�����Ӧ��ˮ�Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺����������ϵ��֮��Ϊ1���Գ�����ͬ����ͼ����y�ύ��Ҳ��ͬ�Ķ��κ�����Ϊ�Ѻ�ͬ����κ���![]() ���磺
���磺![]() ���Ѻ�ͬ����κ���Ϊ
���Ѻ�ͬ����κ���Ϊ![]() ��
��
![]() ����ֱ�д��
����ֱ�д��![]() ��
��![]() ���Ѻ�ͬ����κ�����
���Ѻ�ͬ����κ�����
![]() ����ʲô�����Ķ��κ���û���Ѻ�ͬ����κ���������ʲô�����Ķ��κ������Ѻ�ͬ����κ�������������
����ʲô�����Ķ��κ���û���Ѻ�ͬ����κ���������ʲô�����Ķ��κ������Ѻ�ͬ����κ�������������
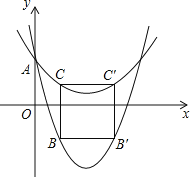
![]() ��ͼ�����κ���
��ͼ�����κ���![]() ��
��![]() �����Ѻ�ͬ����κ���
�����Ѻ�ͬ����κ���![]() ����y�ύ�ڵ�A����B��C�ֱ���
����y�ύ�ڵ�A����B��C�ֱ���![]() ��
��![]() �ϣ���B��C�ĺ������Ϊ
�ϣ���B��C�ĺ������Ϊ![]() �����ǹ���
�����ǹ���![]() �ĶԳ���ĶԳƵ�ֱ�Ϊ
�ĶԳ���ĶԳƵ�ֱ�Ϊ![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ��CB��
��CB��
![]() ��
��![]() �����ı���
�����ı���![]() Ϊ�����Σ���m��ֵ��
Ϊ�����Σ���m��ֵ��
![]() ��
��![]() �����ı���
�����ı���![]() ���ڱ�֮��Ϊ1��2��ֱ��д��a��ֵ��
���ڱ�֮��Ϊ1��2��ֱ��д��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
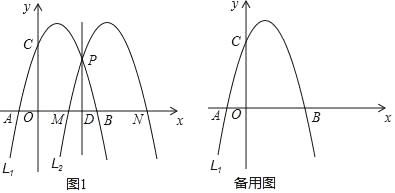
����Ŀ����ͼ1����֪������L1��y=��x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����L1����ȡһ��P������P��ֱ��l��x�ᣬ����ΪD����L1��ֱ��l���۵õ�������L2����x���ڵ�M��N����M�ڵ�N����ࣩ��
��1����L1��L2�غ�ʱ�����P�����ꣻ
��2������P���B�غ�ʱ�����ʱL2�Ľ���ʽ����ֱ��д��L1��L2�У�y����x���������Сʱ��x��ȡֵ��Χ��
��3������PM��PB�����P��m��n������n=![]() mʱ������PMB�������
mʱ������PMB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����̽��ij����κ�������ʱ�����������¹��̣�
�������
(1)��֪������![]() ������(-1,0),��
������(-1,0),��![]() = ����������Ϊ ���������߹��ڵ�(0,1�������ĶԳƵ������ߵı���ʽ�� .
= ����������Ϊ ���������߹��ڵ�(0,1�������ĶԳƵ������ߵı���ʽ�� .
�������
���Ƕ��壺����������![]() ,��
,��![]() ���ϵĵ�
���ϵĵ�![]() Ϊ���ģ����������߹���
Ϊ���ģ����������߹���
��![]() �ԳƵ�������
�ԳƵ�������![]() ,�������ֳ�������
,�������ֳ�������![]() Ϊ������
������![]() ��������������������
��������������������![]() ������������.
������������.
(2)��֪������![]() ���ڵ�
���ڵ�![]() ������������Ϊ
������������Ϊ![]() �����������������н��㣬��
�����������������н��㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
������
(3) ��֪������![]()
����������![]() ������������Ϊ
������������Ϊ![]() ,�����������������㣬��ǡ�������ǵĶ��㣬��
,�����������������㣬��ǡ�������ǵĶ��㣬��![]() ��ֵ���������ĵ����ꣻ
��ֵ���������ĵ����ꣻ
����������![]() ���ڵ�
���ڵ�![]() ������������Ϊ
������������Ϊ![]() ,�䶥��Ϊ
,�䶥��Ϊ![]() �����ڵ�
�����ڵ�![]() ������������Ϊ
������������Ϊ![]() ���䶥��Ϊ
���䶥��Ϊ![]() ���������ڵ�
���������ڵ�![]() ������������Ϊ
������������Ϊ![]() ���䶥��Ϊ
���䶥��Ϊ![]() ����(
����(![]() Ϊ
Ϊ
������).��![]() �ij�(�ú�
�ij�(�ú�![]() ��ʽ�ӱ�ʾ).
��ʽ�ӱ�ʾ).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��
��![]() ��
��![]() �dz�������
�dz�������![]() �е�
�е�![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���ʾ�������н����У���ȷ�ĸ����У� ��
�IJ��ֶ�Ӧֵ���±���ʾ�������н����У���ȷ�ĸ����У� ��
|
|
|
|
|
|
|
|
|
|
![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() ��ֵ��
��ֵ��![]() ֵ���������С��
ֵ���������С��
![]() ����
����![]() ����������ȵ�ʵ������
����������ȵ�ʵ������
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com