
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
阅读题目,先利用待定系数法求得该函数解析式,根据a的值即可判断(1) ;接下来根据函数解析式可得函数对称轴,根据二次函数的性质判断(2)(3) ;对于(4),由y=ax2+bx+c (a,b,c为常数,且a≠0)的图象与x轴有两个交点,顶点坐标的纵坐标>5,可得方程ax2+bx+c=5根的情况,据此判断即可,至此问题得解.
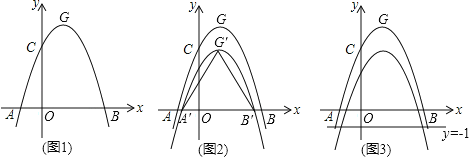
由图表中数据可得出:x=-1时,y=-1,x=0时,y=3,x=1时,y=5,则有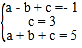 ,解得
,解得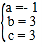 ,则y=-x2+3x+3=-(x-
,则y=-x2+3x+3=-(x-![]() )2+
)2+![]() ,因为a=-1<0,所以(1)正确,因为该函数的对称轴x=
,因为a=-1<0,所以(1)正确,因为该函数的对称轴x=![]() ,所以当x<0时,y<3,故(2)正确,根据二次函数的性质可得到x>
,所以当x<0时,y<3,故(2)正确,根据二次函数的性质可得到x>![]() 时,y的值随x值的增大而减小,x<
时,y的值随x值的增大而减小,x<![]() 时,y的值随x的值的增大而增大,故(3)错误,因为y=ax2+bx+c的图象与x轴有交点,顶点坐标的纵坐标>5,所以方程ax2+bx+c=5,有两个不相等的实数根,故(4)正确,故答案选B.
时,y的值随x的值的增大而增大,故(3)错误,因为y=ax2+bx+c的图象与x轴有交点,顶点坐标的纵坐标>5,所以方程ax2+bx+c=5,有两个不相等的实数根,故(4)正确,故答案选B.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=![]() ,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
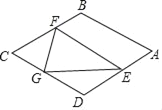
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的斜边
的斜边![]() ,
,![]() .
.
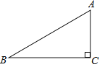
![]() 以点
以点![]() 为圆心作圆,当半径为多长时,直线
为圆心作圆,当半径为多长时,直线![]() 与
与![]() 相切?为什么?
相切?为什么?
![]() 以点
以点![]() 为圆心,分别以
为圆心,分别以![]() 和
和![]() 为半径作两个圆,这两个圆与直线
为半径作两个圆,这两个圆与直线![]() 分别有怎样的位置关系?
分别有怎样的位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有![]() 张床位的旅馆,当每张床位每天收费
张床位的旅馆,当每张床位每天收费![]() 元时,床位可全部租出.若每张床位每天收费提高
元时,床位可全部租出.若每张床位每天收费提高![]() 元,则相应的减少了
元,则相应的减少了![]() 张床位租出.如果每张床位每天以
张床位租出.如果每张床位每天以![]() 元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴相交于
与坐标轴相交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是线段
是线段![]() 上一动点(端点除外),过
上一动点(端点除外),过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
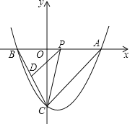
![]() 直接写出
直接写出![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
![]() 求抛物线
求抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 求
求![]() 面积的最大值,并判断当
面积的最大值,并判断当![]() 的面积取最大值时,以
的面积取最大值时,以![]() 、
、![]() 为邻边的平行四边形是否为菱形.
为邻边的平行四边形是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
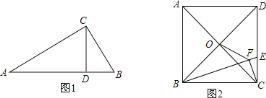
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com