
ЎѕМвДїЎїРЎПНУлРЎЅЬФЪМЅѕїДіАа¶юґОєЇКэОКМвК±Ј¬ѕАъБЛИзПВ№эіМЈє
ЗуЅвМеСй
(1)ТСЦЄЕЧОпПЯ![]() ѕ№эµг(-1,0),Фт
ѕ№эµг(-1,0),Фт![]() = Ј¬¶ҐµгЧш±кОЄ Ј¬ёГЕЧОпПЯ№ШУЪµг(0,1Ј©іЙЦРРД¶ФіЖµДЕЧОпПЯµД±нґпКЅКЗ .
= Ј¬¶ҐµгЧш±кОЄ Ј¬ёГЕЧОпПЯ№ШУЪµг(0,1Ј©іЙЦРРД¶ФіЖµДЕЧОпПЯµД±нґпКЅКЗ .
ійПуёРОт
ОТГЗ¶ЁТеЈє¶ФУЪЕЧОпПЯ![]() ,ТФ
,ТФ![]() ЦбЙПµДµг
ЦбЙПµДµг![]() ОЄЦРРДЈ¬ЧчёГЕЧОпПЯ№ШУЪ
ОЄЦРРДЈ¬ЧчёГЕЧОпПЯ№ШУЪ
µг![]() ¶ФіЖµДЕЧОпПЯ
¶ФіЖµДЕЧОпПЯ![]() ,ФтОТГЗУЦіЖЕЧОпПЯ
,ФтОТГЗУЦіЖЕЧОпПЯ![]() ОЄЕЧОпПЯ
ОЄЕЧОпПЯ![]() µДЎ°СЬЙъЕЧОпПЯЎ±Ј¬µг
µДЎ°СЬЙъЕЧОпПЯЎ±Ј¬µг![]() ОЄЎ°СЬЙъЦРРДЎ±.
ОЄЎ°СЬЙъЦРРДЎ±.
(2)ТСЦЄЕЧОпПЯ![]() №ШУЪµг
№ШУЪµг![]() µДСЬЙъЕЧОпПЯОЄ
µДСЬЙъЕЧОпПЯОЄ![]() Ј¬ИфХвБЅМхЕЧОпПЯУРЅ»µгЈ¬Зу
Ј¬ИфХвБЅМхЕЧОпПЯУРЅ»µгЈ¬Зу![]() µДИЎЦµ·¶О§.
µДИЎЦµ·¶О§.
ОКМвЅвѕц
(3) ТСЦЄЕЧОпПЯ![]()
ўЩИфЕЧОпПЯ![]() µДСЬЙъЕЧОпПЯОЄ
µДСЬЙъЕЧОпПЯОЄ![]() ,БЅЕЧОпПЯУРБЅёцЅ»µгЈ¬ЗТЗЎєГКЗЛьГЗµД¶ҐµгЈ¬Зу
,БЅЕЧОпПЯУРБЅёцЅ»µгЈ¬ЗТЗЎєГКЗЛьГЗµД¶ҐµгЈ¬Зу![]() µДЦµј°СЬЙъЦРРДµДЧш±кЈ»
µДЦµј°СЬЙъЦРРДµДЧш±кЈ»
ўЪИфЕЧОпПЯ![]() №ШУЪµг
№ШУЪµг![]() µДСЬЙъЕЧОпПЯОЄ
µДСЬЙъЕЧОпПЯОЄ![]() ,Ж䶥µгОЄ
,Ж䶥µгОЄ![]() Ј»№ШУЪµг
Ј»№ШУЪµг![]() µДСЬЙъЕЧОпПЯОЄ
µДСЬЙъЕЧОпПЯОЄ![]() Ј¬Ж䶥µгОЄ
Ј¬Ж䶥µгОЄ![]() Ј»ЎЈ»№ШУЪµг
Ј»ЎЈ»№ШУЪµг![]() µДСЬЙъЕЧОпПЯОЄ
µДСЬЙъЕЧОпПЯОЄ![]() Ј¬Ж䶥µгОЄ
Ј¬Ж䶥µгОЄ![]() Ј»Ў(
Ј»Ў(![]() ОЄ
ОЄ
ХэХыКэ).Зу![]() µДі¤(УГє¬
µДі¤(УГє¬![]() µДКЅЧУ±нКѕ).
µДКЅЧУ±нКѕ).

Ўѕґр°ёЎїЗуЅвМеСйЈє ![]() Ј»¶ҐµгЧш±кКЗ(-2,1)Ј»
Ј»¶ҐµгЧш±кКЗ(-2,1)Ј»![]() Ј»ійПуёРОтЈє
Ј»ійПуёРОтЈє![]() Ј»ОКМвЅвѕцЈєўЩ
Ј»ОКМвЅвѕцЈєўЩ![]() Ј»ЈЁ0Ј¬6Ј©Ј»ўЪ
Ј»ЈЁ0Ј¬6Ј©Ј»ўЪ![]()
ЎѕЅвОцЎї(1)°С(-1Ј¬0)ґъИл![]() јґїЙОґіц
јґїЙОґіц![]() =-4Ј¬И»єу°СЕЧОпПЯЅвОцКЅ±дОЄ¶ҐµгКЅјґїЙЗуµГЕЧОпПЯµД¶ҐµгЧш±кЈ¬јМ¶шїЙµГ¶Ґµг№ШУЪЈЁ0Ј¬1Ј©µД¶ФіЖµгЈ¬ґУ¶шїЙРґіцФЕЧОпПЯ№ШУЪµг(0Ј¬1Ј©іЙЦРРД¶ФіЖµДЕЧОпПЯµД±нґпКЅЈ»
=-4Ј¬И»єу°СЕЧОпПЯЅвОцКЅ±дОЄ¶ҐµгКЅјґїЙЗуµГЕЧОпПЯµД¶ҐµгЧш±кЈ¬јМ¶шїЙµГ¶Ґµг№ШУЪЈЁ0Ј¬1Ј©µД¶ФіЖµгЈ¬ґУ¶шїЙРґіцФЕЧОпПЯ№ШУЪµг(0Ј¬1Ј©іЙЦРРД¶ФіЖµДЕЧОпПЯµД±нґпКЅЈ»
ЈЁ2Ј©ПИЗуіцЕЧОпПЯ ![]() µД¶ҐµгКЗЈЁ-1Ј¬6Ј©Ј¬ґУ¶шЗуіц (-1Ј¬6)№ШУЪ
µД¶ҐµгКЗЈЁ-1Ј¬6Ј©Ј¬ґУ¶шЗуіц (-1Ј¬6)№ШУЪ![]() µД¶ФіЖµгКЗ
µД¶ФіЖµгКЗ![]() Ј¬µГ
Ј¬µГ ![]() Ј¬ёщѕЭБЅЕЧОпПЯУРЅ»µгЈ¬їЙТФИ·¶Ё·ЅіМ
Ј¬ёщѕЭБЅЕЧОпПЯУРЅ»µгЈ¬їЙТФИ·¶Ё·ЅіМ ![]() УРЅвЈ¬јМ¶шЗуµГmµДИЎЦµ·¶О§јґїЙЈ»
УРЅвЈ¬јМ¶шЗуµГmµДИЎЦµ·¶О§јґїЙЈ»
(3) ўЩПИЗуіцЕЧОпПЯ![]() ТФј°ЕЧОпПЯ
ТФј°ЕЧОпПЯ![]() µДСЬЙъЕЧОпПЯОЄ
µДСЬЙъЕЧОпПЯОЄ![]() Ј¬µД¶ҐµгЧш±кЈ¬ёщѕЭБЅЕЧОпПЯУРБЅёцЅ»µгЈ¬ЗТЗЎєГКЗЛьГЗµД¶ҐµгЈ¬Зу
Ј¬µД¶ҐµгЧш±кЈ¬ёщѕЭБЅЕЧОпПЯУРБЅёцЅ»µгЈ¬ЗТЗЎєГКЗЛьГЗµД¶ҐµгЈ¬Зу![]() µДЦµј°ФЩёщѕЭЦРµгЧш±к№«КЅјґїЙЗуіцСЬЙъЦРРДµДЧш±кЈ»
µДЦµј°ФЩёщѕЭЦРµгЧш±к№«КЅјґїЙЗуіцСЬЙъЦРРДµДЧш±кЈ»
ўЪ ИзНјЈ¬Йи![]() Ј¬
Ј¬![]() Ў
Ў ![]() Ј¬
Ј¬![]() Ул
Ул![]() Цб·Ц±рПаУЪ
Цб·Ц±рПаУЪ![]() Ј¬
Ј¬![]() Ў
Ў ![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬![]() Ј¬Ў
Ј¬Ў ![]() Ј¬
Ј¬![]() ·Ц±р№ШУЪ
·Ц±р№ШУЪ![]() Ј¬
Ј¬![]() Ў
Ў![]() Ј¬
Ј¬![]() ЦРРД¶ФіЖЈ¬УЙМвТвФтїЙµГ
ЦРРД¶ФіЖЈ¬УЙМвТвФтїЙµГ![]() Ј¬
Ј¬![]() Ў
Ў ![]() ·Ц±рКЗЎч
·Ц±рКЗЎч![]() Ј¬
Ј¬![]() Ў
Ў![]() µДЦРО»ПЯЈ¬јМ¶шїЙµГ
µДЦРО»ПЯЈ¬јМ¶шїЙµГ![]() Ј¬
Ј¬![]() Ј¬Ў
Ј¬Ў ![]() Ј¬ФЩёщѕЭµгµДЧш±кјґїЙЗуµГ
Ј¬ФЩёщѕЭµгµДЧш±кјґїЙЗуµГ![]() µДі¤.
µДі¤.
ЗуЅвМеСй
(1)°С(-1Ј¬0)ґъИл![]() µГ
µГ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа¶ҐµгЧш±кКЗ(-2Ј¬1)Ј¬
ЎЯ(-2Ј¬1)№ШУЪ(0Ј¬1)µД¶ФіЖµгКЗ(2Ј¬1)Ј¬
ЎаіЙЦРРД¶ФіЖµДЕЧОпПЯ±нґпКЅКЗЈє![]() Ј¬
Ј¬
јґ ![]() (ИзНј)
(ИзНј)

ійПуёРОт
(2) ЎЯ ![]() Ј¬
Ј¬
Ўа ¶ҐµгКЗЈЁ-1Ј¬6Ј©Ј¬
ЎЯ (-1Ј¬6)№ШУЪ![]() µД¶ФіЖµгКЗ
µД¶ФіЖµгКЗ![]() Ј¬
Ј¬
Ўа ![]() Ј¬
Ј¬
ЎЯ БЅЕЧОпПЯУРЅ»µгЈ¬
Ўа ![]() УРЅвЈ¬
УРЅвЈ¬
Ўа ![]() УРЅвЈ¬
УРЅвЈ¬
Ўа ![]() Ј¬
Ј¬
Ўа ![]() Ј»(ИзНј)
Ј»(ИзНј)
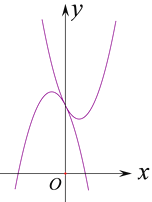
ОКМвЅвѕц
(3) ўЩ ЎЯ![]() =
=![]() Ј¬
Ј¬
Ўа ¶ҐµгЈЁ-1Ј¬![]() Ј©Ј¬
Ј©Ј¬
ґъИл ![]() µГЈє
µГЈє![]() ўЩ
ўЩ
ЎЯ ![]() Ј¬
Ј¬
Ўа ¶ҐµгЈЁ1Ј¬![]() Ј©Ј¬
Ј©Ј¬
ґъИл ![]() µГЈє
µГЈє![]() ўЪ
ўЪ
УЙўЩ ўЪ µГ ![]() Ј¬
Ј¬
ЎЯ ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа ![]() Ј¬
Ј¬
Ўа БЅ¶ҐµгЧш±к·Ц±рКЗЈЁ-1Ј¬0Ј©Ј¬ЈЁ1Ј¬12Ј©Ј¬
УЙЦРµгЧш±к№«КЅµГЎ°СЬЙъЦРРДЎ±µДЧш±кКЗЈЁ0Ј¬6Ј©Ј»
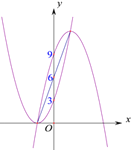
ўЪ ИзНјЈ¬Йи![]() Ј¬
Ј¬![]() Ў
Ў ![]() Ј¬
Ј¬![]() Ул
Ул![]() Цб·Ц±рПаУЪ
Цб·Ц±рПаУЪ![]() Ј¬
Ј¬![]() Ў
Ў ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Фт![]() Ј¬
Ј¬![]() Ј¬Ў
Ј¬Ў ![]() Ј¬
Ј¬![]() ·Ц±р№ШУЪ
·Ц±р№ШУЪ![]() Ј¬
Ј¬![]() Ў
Ў![]() Ј¬
Ј¬![]() ЦРРД¶ФіЖЈ¬
ЦРРД¶ФіЖЈ¬
Ўа![]() Ј¬
Ј¬![]() Ў
Ў ![]() ·Ц±рКЗЎч
·Ц±рКЗЎч![]() Ј¬
Ј¬![]() Ў
Ў![]() µДЦРО»ПЯЈ¬
µДЦРО»ПЯЈ¬
Ўа![]() Ј¬
Ј¬![]() Ј¬Ў
Ј¬Ў ![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
Ўа![]()
![]() ]
]![]() .
.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬A(0Ј¬3)ЎўB(3Ј¬0)Ј¬ТФµгBОЄФІРДЎў2ОЄ°лѕ¶µДЎСBЙПУРТ»¶ЇµгPЈ®Б¬ЅУAPЈ¬ИфµгCОЄAPµДЦРµгЈ¬Б¬ЅУOCЈ¬ФтOCµДЧоРЎЦµОЄ(ЎЎЎЎ)
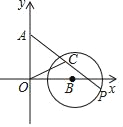
A. 1 B. ![]() ©Ѓ1 C.
©Ѓ1 C. ![]() D. 2
D. 2![]() ©Ѓ1
©Ѓ1
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬ЕЧОпПЯC1Јєy=ax2©Ѓ2ax+cЈЁaЈј0Ј©УлxЦбЅ»УЪAЎўBБЅµгЈ¬УлyЦбЅ»УЪµгCЈ®ТСЦЄµгAµДЧш±кОЄЈЁ©Ѓ1Ј¬0Ј©Ј¬µгOОЄЧш±кФµгЈ¬OC=3OAЈ¬ЕЧОпПЯC1µД¶ҐµгОЄGЈ®
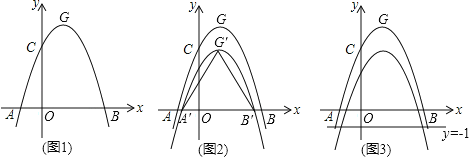
ЈЁ1Ј©ЗуіцЕЧОпПЯC1µДЅвОцКЅЈ¬ІўРґіцµгGµДЧш±кЈ»
ЈЁ2Ј©ИзНј2Ј¬Ѕ«ЕЧОпПЯC1ПтПВЖЅТЖkЈЁkЈѕ0Ј©ёцµҐО»Ј¬µГµЅЕЧОпПЯC2Ј¬ЙиC2УлxЦбµДЅ»µгОЄAЎдЎўBЎдЈ¬¶ҐµгОЄGЎдЈ¬µ±ЎчAЎдBЎдGЎдКЗµИ±ЯИэЅЗРОК±Ј¬ЗуkµДЦµЈє
ЈЁ3Ј©ФЪЈЁ2Ј©µДМхјюПВЈ¬ИзНј3Ј¬ЙиµгMОЄxЦбХэ°лЦбЙПТ»¶ЇµгЈ¬№эµгMЧчxЦбµДґ№ПЯ·Ц±рЅ»ЕЧОпПЯC1ЎўC2УЪPЎўQБЅµгЈ¬КФМЅѕїФЪЦ±ПЯy=©Ѓ1ЙПКЗ·сґжФЪµгNЈ¬К№µГТФPЎўQЎўNОЄ¶ҐµгµДИэЅЗРОУлЎчAOQИ«µИЈ¬ИфґжФЪЈ¬Ц±ЅУРґіцµгMЈ¬NµДЧш±кЈєИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬![]() Ј¬
Ј¬![]() КЗ
КЗ![]() ЙПµДТ»µгЈ¬
ЙПµДТ»µгЈ¬![]() Ј¬µг
Ј¬µг![]() ОЄ
ОЄ![]() ЙПµДТ»¶ЇµгЈ¬µг
ЙПµДТ»¶ЇµгЈ¬µг![]() ОЄ
ОЄ![]() ЙПµДТ»¶ЇµгЈ¬Фт
ЙПµДТ»¶ЇµгЈ¬Фт![]() µДЧоРЎЦµОЄ ________Ј¬µ±
µДЧоРЎЦµОЄ ________Ј¬µ±![]() µДЦµИЎЧоРЎЦµК±Ј¬Фт
µДЦµИЎЧоРЎЦµК±Ј¬Фт![]() µДГж»эОЄ________.
µДГж»эОЄ________.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
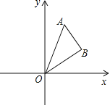
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ОТГЗ¶ЁТеЦ±ПЯ![]() ОЄЕЧОпПЯ
ОЄЕЧОпПЯ![]() ЎўbЎўcОЄіЈКэЈ¬
ЎўbЎўcОЄіЈКэЈ¬![]() µДЎ°ГОПлЦ±ПЯЎ±Ј»УРТ»ёц¶ҐµгФЪЕЧОпПЯЙПЈ¬БнУРТ»ёц¶ҐµгФЪyЦбЙПµДИэЅЗРООЄЖдЎ°ГОПлИэЅЗРОЎ±Ј®
µДЎ°ГОПлЦ±ПЯЎ±Ј»УРТ»ёц¶ҐµгФЪЕЧОпПЯЙПЈ¬БнУРТ»ёц¶ҐµгФЪyЦбЙПµДИэЅЗРООЄЖдЎ°ГОПлИэЅЗРОЎ±Ј®

ТСЦЄЕЧОпПЯ![]() УлЖдЎ°ГОПлЦ±ПЯЎ±Ѕ»УЪAЎўBБЅµг
УлЖдЎ°ГОПлЦ±ПЯЎ±Ѕ»УЪAЎўBБЅµг![]() µгAФЪµгBµДЧуІа
µгAФЪµгBµДЧуІа![]() Ј¬УлxЦбёє°лЦбЅ»УЪµгCЈ®
Ј¬УлxЦбёє°лЦбЅ»УЪµгCЈ®
![]() МоїХЈєёГЕЧОпПЯµДЎ°ГОПлЦ±ПЯЎ±µДЅвОцКЅОЄ______Ј¬µгAµДЧш±кОЄ______Ј¬µгBµДЧш±кОЄ______Ј»
МоїХЈєёГЕЧОпПЯµДЎ°ГОПлЦ±ПЯЎ±µДЅвОцКЅОЄ______Ј¬µгAµДЧш±кОЄ______Ј¬µгBµДЧш±кОЄ______Ј»
![]() ИзНјЈ¬µгMОЄПЯ¶ОCBЙПТ»¶ЇµгЈ¬Ѕ«
ИзНјЈ¬µгMОЄПЯ¶ОCBЙПТ»¶ЇµгЈ¬Ѕ«![]() ТФAMЛщФЪЦ±ПЯОЄ¶ФіЖЦб·ХЫЈ¬µгCµД¶ФіЖµгОЄNЈ¬Иф
ТФAMЛщФЪЦ±ПЯОЄ¶ФіЖЦб·ХЫЈ¬µгCµД¶ФіЖµгОЄNЈ¬Иф![]() ОЄёГЕЧОпПЯµДЎ°ГОПлИэЅЗРОЎ±Ј¬ЗуµгNµДЧш±кЈ»
ОЄёГЕЧОпПЯµДЎ°ГОПлИэЅЗРОЎ±Ј¬ЗуµгNµДЧш±кЈ»
![]() µ±µгEФЪЕЧОпПЯµД¶ФіЖЦбЙПФЛ¶ЇК±Ј¬ФЪёГЕЧОпПЯµДЎ°ГОПлЦ±ПЯЎ±ЙПЈ¬КЗ·сґжФЪµгFЈ¬К№µГТФµгAЎўCЎўEЎўFОЄ¶ҐµгµДЛД±ЯРООЄЖЅРРЛД±ЯРОЈїИфґжФЪЈ¬ЗлЦ±ЅУРґіцµгEЎўFµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
µ±µгEФЪЕЧОпПЯµД¶ФіЖЦбЙПФЛ¶ЇК±Ј¬ФЪёГЕЧОпПЯµДЎ°ГОПлЦ±ПЯЎ±ЙПЈ¬КЗ·сґжФЪµгFЈ¬К№µГТФµгAЎўCЎўEЎўFОЄ¶ҐµгµДЛД±ЯРООЄЖЅРРЛД±ЯРОЈїИфґжФЪЈ¬ЗлЦ±ЅУРґіцµгEЎўFµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬µг
ЦРЈ¬µг![]() Ј¬µг
Ј¬µг![]() Ј¬Ѕ«
Ј¬Ѕ«![]() ИЖЧЕµг
ИЖЧЕµг![]() РэЧЄ
РэЧЄ![]() єуµГµЅ
єуµГµЅ![]() Ј®
Ј®
![]() ФЪНјЦР»іц
ФЪНјЦР»іц![]() Ј»
Ј»
![]() µг
µг![]() Ј¬µг
Ј¬µг![]() µД¶ФУ¦µг
µД¶ФУ¦µг![]() ЎЇєН
ЎЇєН![]() ЎЇµДЧш±к·Ц±рКЗ
ЎЇµДЧш±к·Ц±рКЗ![]() ЎЇ________єН
ЎЇ________єН![]() ЎЇ________Ј»
ЎЇ________Ј»
![]() ЗлЦ±ЅУРґіц
ЗлЦ±ЅУРґіц![]() єН
єН![]() ЎЇ
ЎЇ![]() ЎЇµДКэБї№ШПµєНО»ЦГ№ШПµЈ®
ЎЇµДКэБї№ШПµєНО»ЦГ№ШПµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
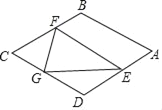
ЎѕМвДїЎїИзНјЈ¬ФЪБвРОABCDЦРЈ¬AB=![]() Ј¬ЎПB=120ЎгЈ¬µгEКЗAD±ЯЙПµДТ»ёц¶ЇµгЈЁІ»УлAЈ¬DЦШєПЈ©Ј¬EFЎОABЅ»BCУЪµгFЈ¬µгGФЪCDЙПЈ¬DG=DEЈ®ИфЎчEFGКЗµИСьИэЅЗРОЈ¬ФтDEµДі¤ОЄ_____Ј®
Ј¬ЎПB=120ЎгЈ¬µгEКЗAD±ЯЙПµДТ»ёц¶ЇµгЈЁІ»УлAЈ¬DЦШєПЈ©Ј¬EFЎОABЅ»BCУЪµгFЈ¬µгGФЪCDЙПЈ¬DG=DEЈ®ИфЎчEFGКЗµИСьИэЅЗРОЈ¬ФтDEµДі¤ОЄ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
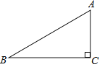
ЎѕМвДїЎїИзНјЈ¬ТСЦЄ![]() µДР±±Я
µДР±±Я![]() Ј¬
Ј¬![]() Ј®
Ј®
![]() ТФµг
ТФµг![]() ОЄФІРДЧчФІЈ¬µ±°лѕ¶ОЄ¶аі¤К±Ј¬Ц±ПЯ
ОЄФІРДЧчФІЈ¬µ±°лѕ¶ОЄ¶аі¤К±Ј¬Ц±ПЯ![]() Ул
Ул![]() ПаЗРЈїОЄКІГґЈї
ПаЗРЈїОЄКІГґЈї
![]() ТФµг
ТФµг![]() ОЄФІРДЈ¬·Ц±рТФ
ОЄФІРДЈ¬·Ц±рТФ![]() єН
єН![]() ОЄ°лѕ¶ЧчБЅёцФІЈ¬ХвБЅёцФІУлЦ±ПЯ
ОЄ°лѕ¶ЧчБЅёцФІЈ¬ХвБЅёцФІУлЦ±ПЯ![]() ·Ц±рУРФхСщµДО»ЦГ№ШПµЈї
·Ц±рУРФхСщµДО»ЦГ№ШПµЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
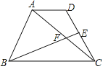
ЎѕМвДїЎїИзНјЈ¬ФЪМЭРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬µг
Ј¬µг![]() КЗ
КЗ![]() µДЦРµгЈ¬
µДЦРµгЈ¬![]() Ул
Ул![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј¬ДЗГґ
Ј¬ДЗГґ![]() єН
єН![]() µДГж»э±ИКЗ____Ј®
µДГж»э±ИКЗ____Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com