
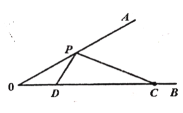
【题目】如图,![]() ,
,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 为
为![]() 上的一动点,点
上的一动点,点![]() 为
为![]() 上的一动点,则
上的一动点,则![]() 的最小值为 ________,当
的最小值为 ________,当![]() 的值取最小值时,则
的值取最小值时,则![]() 的面积为________.
的面积为________.
【答案】2![]()
![]()
【解析】
作D点关于AO的对称点D’,当C,P,D’在同一直线上时,![]() 取最小值,则CD’=
取最小值,则CD’=![]() ,故当CD’⊥OD’时,CD’最小,根据
,故当CD’⊥OD’时,CD’最小,根据![]() 得到∠BOD’=60°,根据OC=4,利用三角函数即可求出此时的CD’;作PH⊥BO,根据角平分线的性质得到DP’=PH,根据Rt△OPD’求出D’P,再根据三角形的面积公式即可求出
得到∠BOD’=60°,根据OC=4,利用三角函数即可求出此时的CD’;作PH⊥BO,根据角平分线的性质得到DP’=PH,根据Rt△OPD’求出D’P,再根据三角形的面积公式即可求出![]() 的面积.
的面积.
作D点关于AO的对称点D’,当C,P,D’在同一直线上时,![]() 取最小值,
取最小值,
故当CD’⊥OD’时,CD’最小,
如图,∵![]()
∴∠BOD’=60°,
∵OC=4,
∴CD’=OCsin60°=4×![]() =2
=2![]() ,
,
故![]() 的最小值为2
的最小值为2![]() ;
;
过PH⊥OC,
∵OP平分∠COD’
∴PH=D’P
∵OD’=OCcos60°=4×![]() =2,
=2,
∴DP’=OD’tan30°=2×![]() =
=![]()
故PH=![]()
∴此时S△OPC=![]() OC×PH=
OC×PH=![]() ×4×
×4×![]() =
=![]()
故答案为:2![]() ;
;![]() .
.



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
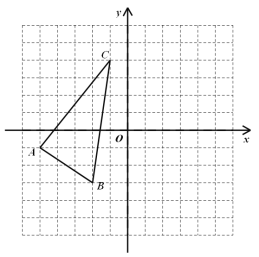
(1)按要求作图: △ABC关于![]() 轴对称的图形△
轴对称的图形△![]() ;
;
(2)将点![]() 先向上平移
先向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得到点
个单位得到点![]() 的坐标为 ;
的坐标为 ;
(3)△![]() 的面积为 ;
的面积为 ;
(4)若![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]()
![]() ,则△
,则△![]() 周长的最小值为 .
周长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+k+1的图象与一次函数y=﹣x+4的图象交于点A(1,a).

(1)求a、k的值;
(2)根据图象,写出不等式﹣x+4>kx+k+1的解;
(3)结合图形,当x>2时,求一次函数y=﹣x+4函数值y的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数![]() 例如:
例如:![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() .
.
![]() 请你分别写出
请你分别写出![]() ,
,![]() 的友好同轴二次函数;
的友好同轴二次函数;
![]() 满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
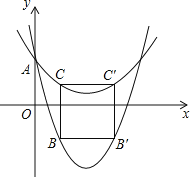
![]() 如图,二次函数
如图,二次函数![]() :
:![]() 与其友好同轴二次函数
与其友好同轴二次函数![]() 都与y轴交于点A,点B、C分别在
都与y轴交于点A,点B、C分别在![]() 、
、![]() 上,点B,C的横坐标均为
上,点B,C的横坐标均为![]() ,它们关于
,它们关于![]() 的对称轴的对称点分别为
的对称轴的对称点分别为![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,CB.
,CB.
![]() 若
若![]() ,且四边形
,且四边形![]() 为正方形,求m的值;
为正方形,求m的值;
![]() 若
若![]() ,且四边形
,且四边形![]() 的邻边之比为1:2,直接写出a的值.
的邻边之比为1:2,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
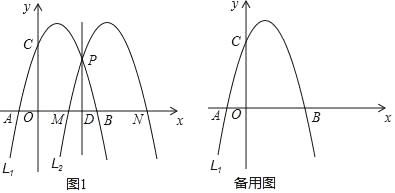
【题目】如图1,已知抛物线L1:y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,在L1上任取一点P,过点P作直线l⊥x轴,垂足为D,将L1沿直线l翻折得到抛物线L2,交x轴于点M,N(点M在点N的左侧).
(1)当L1与L2重合时,求点P的坐标;
(2)当点P与点B重合时,求此时L2的解析式;并直接写出L1与L2中,y均随x的增大而减小时的x的取值范围;
(3)连接PM,PB,设点P(m,n),当n=![]() m时,求△PMB的面积.
m时,求△PMB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:我们可以将任意三位数记为![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分别表示该数的百位数字,十位数字和个位数字,且
分别表示该数的百位数字,十位数字和个位数字,且![]() ),显然
),显然![]() .
.
材料二:若一个三位数的百位数字,十位数字和个位数字均不为0,则称之为初始数,比如123就是一个初始数,将初始数的三个数位上的数字交换顺序,可产生出5个新的初始数,比如由123可以产生出132,213,231,312,321这5个新初始数,这6个初始数的和成为终止数.
(1)求初始数125生成的终止数;
(2)若一个初始数![]() ,满足
,满足![]() ,且
,且![]() ,记
,记![]() ,
,![]() ,
,![]() ,若
,若![]() ,求满足条件的初始数的值.
,求满足条件的初始数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验
(1)已知抛物线![]() 经过点(-1,0),则
经过点(-1,0),则![]() = ,顶点坐标为 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式是 .
= ,顶点坐标为 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式是 .
抽象感悟
我们定义:对于抛物线![]() ,以
,以![]() 轴上的点
轴上的点![]() 为中心,作该抛物线关于
为中心,作该抛物线关于
点![]() 对称的抛物线
对称的抛物线![]() ,则我们又称抛物线
,则我们又称抛物线![]() 为抛物线
为抛物线![]() 的“衍生抛物线”,点
的“衍生抛物线”,点![]() 为“衍生中心”.
为“衍生中心”.
(2)已知抛物线![]() 关于点
关于点![]() 的衍生抛物线为
的衍生抛物线为![]() ,若这两条抛物线有交点,求
,若这两条抛物线有交点,求![]() 的取值范围.
的取值范围.
问题解决
(3) 已知抛物线![]()
①若抛物线![]() 的衍生抛物线为
的衍生抛物线为![]() ,两抛物线有两个交点,且恰好是它们的顶点,求
,两抛物线有两个交点,且恰好是它们的顶点,求![]() 的值及衍生中心的坐标;
的值及衍生中心的坐标;
②若抛物线![]() 关于点
关于点![]() 的衍生抛物线为
的衍生抛物线为![]() ,其顶点为
,其顶点为![]() ;关于点
;关于点![]() 的衍生抛物线为
的衍生抛物线为![]() ,其顶点为
,其顶点为![]() ;…;关于点
;…;关于点![]() 的衍生抛物线为
的衍生抛物线为![]() ,其顶点为
,其顶点为![]() ;…(
;…(![]() 为
为
正整数).求![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图①),图②是平面图.光明中学的数学兴趣小组针对风电塔杆进行了测量,甲同学站在平地上的A处测得塔杆顶端C的仰角是55°,乙同学站在岩石B处测得叶片的最高位置D的仰角是45°(D,C,H在同一直线上,G,A,H在同一条直线上),他们事先从相关部门了解到叶片的长度为15米(塔杆与叶片连接处的长度忽略不计),岩石高BG为4米,两处的水平距离AG为23米,BG⊥GH,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com