
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 18000元 |
| 第二周 | 4台 | 10台 | 31000元 |
分析 (1)设A、B两种型号净水器的销售单价分别为x元、y元,根据3台A型号5台B型号的净水器收入18000元,4台A型号10台B型号的净水器收入31000元,列方程组求解;
(2)设采购A种型号净水器a台,则采购B种型号净水器(30-a)台,根据金额不多余54000元,列不等式求解;
(3)设利润为12800元,列方程求出a的值为8,符合(2)的条件,可知能实现目标.
解答 解:(1)设A、B两种净水器的销售单价分别为x元、y元,
依题意得:$\left\{\begin{array}{l}3x+5y=18000\\ 4x+10y=31000\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=2500\\ y=2100\end{array}\right.$.
答:A、B两种净水器的销售单价分别为2500元、2100元.
(2)设采购A种型号净水器a台,则采购B种净水器(30-a)台.
依题意得:2000a+1700(30-a)≤54000,
解得:a≤10.
故超市最多采购A种型号净水器10台时,采购金额不多于54000元.
(3)依题意得:(2500-2000)a+(2100-1700)(30-a)=12800,
解得:a=8,
故采购A种型号净水器8台,采购B种型号净水器22台,公司能实现利润12800元的目标.
点评 本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.


科目:初中数学 来源: 题型:选择题
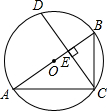 如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )| A. | 6 | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
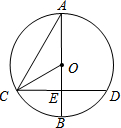 如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )
如图,⊙O的直径AB与弦CD(不是直径)交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com