
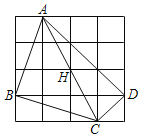
【题目】如图,在4×4的网格中,点A,B,C,D,H均在网格的格点上,下面结论:
①点H是△ABD的内心
②点H是△ABD的外心
③点H是△BCD的外心
④点H是△ADC的外心
其中正确的有( )
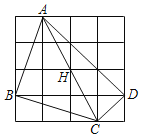
A.1个B.2个C.3个D.4个
【答案】C
【解析】
先利用勾股定理计算出AB=BC=![]() ,AD=
,AD=![]() ,CD=
,CD=![]() ,AC=
,AC=![]() ,再利用勾股定理的逆定理可得到∠ABC=∠ADC=90°,则CB⊥AB,CD⊥AD,根据角平分线定理的逆定理可判断点C不在∠BAD的角平分线上,则根据三角形内心的定义可对①进行判断;由于HA=HB=HC=HD=
,再利用勾股定理的逆定理可得到∠ABC=∠ADC=90°,则CB⊥AB,CD⊥AD,根据角平分线定理的逆定理可判断点C不在∠BAD的角平分线上,则根据三角形内心的定义可对①进行判断;由于HA=HB=HC=HD=![]() ,则根据三角形外心的定义可对②③④进行判断.
,则根据三角形外心的定义可对②③④进行判断.
解:∵AB=BC=![]() ,AD=
,AD=![]() ,CD=
,CD=![]() ,AC=
,AC=![]() ,
,
∴AB2+BC2=AC2,CD2+AD2=AC2,
∴△ABC和△ADC都为直角三角形,∠ABC=∠ADC=90°,
∵CB⊥AB,CD⊥AD,而CB≠CD,
∴点C不在∠BAD的角平分线上,
∴点H不是△ABD的内心,所以①错误;
∵HA=HB=HC=HD=![]() ,
,
∴点H是△ABD的外心,点H是△BCD的外心,点H是△ADC的外心,所以②③④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】若x=﹣m和x=m﹣4时,多项式ax2+bx+4a+1的值相等,且m≠2.当﹣1<x<2时,存在x的值,使多项式ax2+bx+4a+1的值为3,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生产某种农产品的成本每千克20元,调查发现,该产品每天销售量y(千克)与销售单价x(元/千克)满足如下关系:![]() ,设这种农产品的销售利润为w元.
,设这种农产品的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)物价部门规定这种产品的销售价不得高于每千克28元,该农户想在这种产品经销季节每天获得150元的利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某特产专卖店的销售某种特产,其进价为每千克40元,若按每千克60元出售,则平均每天可售出100千克,后来经过市场调查发现,单价每降低3元,平均每天的销售量增加30千克,若专卖店销售这种特产想要平均每天获利2240元,且销量尽可能大,则每千克特产应定价多少元?
(1)方法1:设每千克特产应降价x元,由题意,得方程为:___.
方法2:设每千克特产降价后定价为x元,由题意,得方程为:___.
(2)请你选择一种方法完成解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式ax2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
ax2+bx+c | … | 3 |
| ﹣1 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=ax2+bx+c,则当x取何值时,y<0;
(3)当0<x<3,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个小球上分别标有数字﹣2,﹣1,3,它们除数字外其余全部相同,现将它们放在一个不透明的袋子里,从袋子中随机地摸出一球,将球上的数字记录,记为m,然后放回;再随机地摸取一球,将球上的数字记录,记为n,这样确定了点(m,n).
(1)请列表或画出树状图,并根据列表或树状图写出点(m,n)所有可能的结果;
(2)求点(m,n)在函数y=x的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.4 | 4.3 | ||
卡路里消耗(千卡) | 157 | 79 | 91 | 127 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
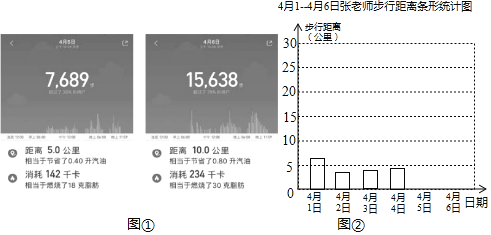
(1)请你将手环记录的4月5日和4月6日的数据(如图①)填入表格
(2)请你将条形统计图(如图②)补充完整
(3)张老师这6天平均每天步行约______公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为______公里(精确到0.1公里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线l:y=kx+m交y轴于点C,与抛物线y=ax2+bx交于点A(4,0)、B(-![]() ,-
,-![]() ).
).
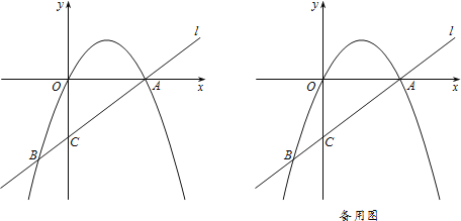
(1)直线l的表达式为:______,抛物线的表达式为:______;
(2)若点P是二次函数y=ax2+bx在第四象限内的图象上的一点,且2S△APB=S△AOB,求△AOP的面积;
(3)若点Q是二次函数图象上一点,设点Q到直线l的距离为d,到抛物线的对称轴的距离为d1,当|d-d1|=2时,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)该公司营销员销售该品牌电脑的月销售平均数是 台,中位数是 台,众数是 台.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com