
【题目】周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象. 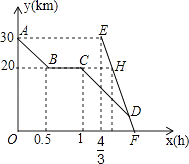
(1)小芳骑车的速度为km/h,H点坐标 .
(2)小芳从家出发多少小时后被妈妈追上?此时距家的路程多远?
(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分钟到达乙地?
【答案】
(1)20;( ![]() ,20)
,20)
(2)解:设直线AB的解析式为:y1=k1x+b1,
将点A(0,30),B(0.5,20)代入得:y1=﹣20x+30,
∵AB∥CD,
∴设直线CD的解析式为:y2=﹣20x+b2,
将点C(1,20)代入得:b2=40,
故y2=﹣20x+40,
设直线EF的解析式为:y3=k3x+b3,
将点E( ![]() ,30),H(
,30),H( ![]() ,20)代入得:k3=﹣60,b3=110,
,20)代入得:k3=﹣60,b3=110,
∴y3=﹣60x+110,
解方程组 ![]() ,得
,得 ![]() ,
,
∴点D坐标为(1.75,5),
30﹣5=25(km),
所以小芳出发1.75小时后被妈妈追上,此时距家25km
(3)解:将y=0代入直线CD解析式有:﹣20x+40=0,
解得x=2,
将y=0代入直线EF的解析式有:﹣60x+110=0,
解得x= ![]() ,
,
2﹣ ![]() =
= ![]() (h)=10(分钟),
(h)=10(分钟),
故小芳比预计时间早10分钟到达乙地
【解析】解:(1)由函数图可以得出,小芳家距离甲地的路程为10km,花费时间为0.5h, 故小芳骑车的速度为:10÷0.5=20(km/h),
由题意可得出,点H的纵坐标为20,横坐标为: ![]() +
+ ![]() =
= ![]() ,
,
故点H的坐标为( ![]() ,20);
,20);


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr)
(1)把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,点A表示的数是;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:
+2,﹣1,﹣5,+4,+3,﹣2
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?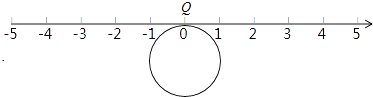
查看答案和解析>>
科目:初中数学 来源: 题型:
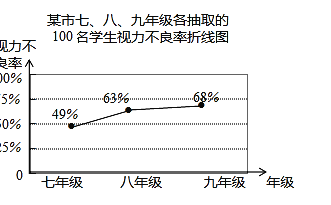
【题目】为了解某市12000名初中学生的视力情况,该校数学兴趣小组从该市七、八、九年级各随机抽取了100名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
(1)由统计图可以看出年级越高视力不良率越 (填“高”或“低”);
(2)抽取的八年级学生中,视力不良的学生有 名;
(3)请你根据抽样调查的结果,估计该市12000名初中学生中视力不良的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个图形平移后,它各点的横、纵坐标都发生变化
B. 一个图形平移后,它的大小发生变化,形状不变
C. 把一个图形沿y轴平移若干个单位长度后,与原图形相比各点的横坐标没有发生变化
D. 图形平移后,一些点的坐标可以不发生变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别过反比例函数y=![]() 的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1,A2,…,An…,连接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A 2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,点B2的纵坐标是____.依此类推,则点Bn的纵坐标是_______.(结果用含n代数式表示)
的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1,A2,…,An…,连接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A 2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,点B2的纵坐标是____.依此类推,则点Bn的纵坐标是_______.(结果用含n代数式表示)
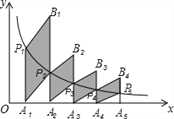
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com