练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

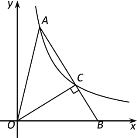
    【题目】如图，在平面直角坐标系中，O为原点，点A在第一象限，点B是x轴正半轴上一点，∠OAB45°，双曲线过点A，交AB于点C，连接OC，若OC⊥AB，则tan∠ABO的值是_____．

    【答案】

    【解析】

    过点C作CE垂直x轴，CD垂直AD，设点A的和点C的坐标，根据“AAS”证明△CEO≌△ADC，求出点A、C的坐标与k的关系，从而求出tan∠ABO的值.

    作CE⊥x轴，AD⊥CD

    则∠D=∠OEC，∠ACD=∠COE

    ∵∠OAB45°

    ∴AC=OC

    ∴△CEO≌△ADC

    ∴AD=CE,CD=OE

    设AD=,CD=b

    可知点A的坐标为（），点C的坐标为（）

    可得

    ∴

    ∴

    ∴或（舍），

    ∵∠ABO+∠BCE=∠BCE+∠OCE=90°，

    ∴∠ABO=∠OCE

    ∴tan∠ABO=tan∠OCE=

    故答案是：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

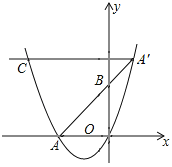
    【题目】如图，在平面直角坐标系中，抛物线y=x2+mx交x轴的负半轴于点A．点B是y轴正半轴上一点，点A关于点B的对称点A′恰好落在抛物线上．过点A′作x轴的平行线交抛物线于另一点C．若点A′的横坐标为1，则A′C的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②当x＞﹣1时，y随x增大而减小；③a+b+c＜0；④若方程ax2+bx+c﹣m=0没有实数根，则m＞2；　⑤3a+c＜0．其中正确结论的个数是（　　）

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y＝﹣x+4与两坐标轴交于P，Q两点，在线段PQ上有一动点A（点A不与P，Q重合），过点A分别作两坐标轴的垂线，垂足为B，C，则下列说法不正确的是（　　）

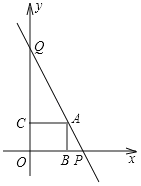
    A.点A的坐标为（2，2）时，四边形OBAC为正方形

    B.在整个运动过程中，四边形OBAC的周长保持不变

    C.四边形OBAC面积的最大值为4

    D.当四边形OBAC的面积为3时，点A的坐标为（1，3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中， ，点分别是边、的中点，将绕着点旋转，点旋转后的对应点分别为点，当直线经过点时，线段的长为____________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△中，，；若将△ 绕点逆时针旋转60°到△ 的位置，连接,则的长为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

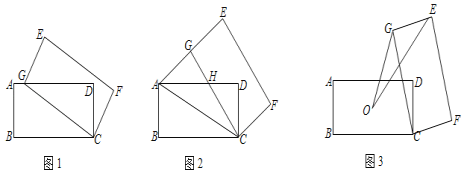
    【题目】矩形ABCD中，AB＝2，AD＝4，将矩形ABCD绕点C顺时针旋转至矩形EGCF（其中E、G、F分别与A、B、D对应）．

    （1）如图1，当点G落在AD边上时，直接写出AG的长为　 　；

    （2）如图2，当点G落在线段AE上时，AD与CG交于点H，求GH的长；

    （3）如图3，记O为矩形ABCD对角线的交点，S为△OGE的面积，求S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共60个，它们除颜色不同外，其余都相同，王颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中搅匀，经过大量重复上述摸球的过程，发现摸到白球的频率定于0.25．

    （1）请估计摸到白球的概率将会接近________；

    （2）计算盒子里白、黑两种颜色的球各有多少个？

    （3）如果要使摸到白球的概率为，需要往盒子里再放入多少个白球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】万州区中小学社会活动实践基地开展了人与社会、人与自然、人与自我的综合实践活动，其中高空项目能培养学生不怕困难，不畏艰险的精神．在高空项目中有以下四个特色实践活动：“A．合力制胜，B．空中断桥，C．绝壁飞胎，D．天罗地网”．为了解学生最喜爱哪项综合实践活动，随机抽取部分学生进行问卷调查（每位学生只能选择一项），将调查结果绘制成下面两幅不完整的统计图，请结合图中提供的信息回答下列问题：

    （1）本次一共调查了　 　名学生，并补全条形统计图；

    （2）现有最喜爱A，B，C，D活动项目的学生各一人，学校要从这四人中随机选取两人交流活动体会，请用列表或画树状图的方法求出恰好选取最喜爱C和D项目的两位学生的概率．

    查看答案和解析>>

    同步练习册答案