
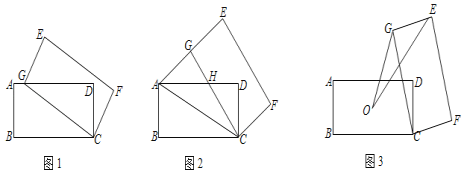
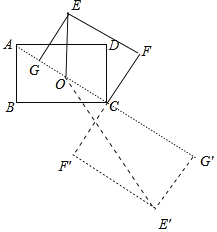
【题目】矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).
(1)如图1,当点G落在AD边上时,直接写出AG的长为 ;
(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;
(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.
【答案】(1)4﹣2![]() ;(2)
;(2)![]() ;(3)4﹣
;(3)4﹣![]() ≤S≤4+
≤S≤4+![]()
【解析】
(1)在Rt△DCG中,利用勾股定理求出DG即可解决问题;
(2)首先证明AH=CH,设AH=CH=m,则DH=AD﹣HD=4﹣m,在Rt△DHC中,根据CH2=CD2+DH2,构建方程求出m即可解决问题;
(3)如图,当点G在对角线AC上时,△OGE的面积最小,当点G在AC的延长线上时,△OE′G′的面积最大,分别求出面积的最小值,最大值即可解决问题.
解:(1)如图1中,
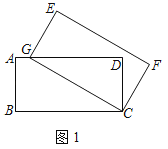
∵四边形ABCD是矩形,
∴BC=AD=CG=4,∠D=90°,
∵AB=CD=2,
∴DG=![]() =
=![]() =2
=2![]() ,
,
∴AG=AB﹣BG=4﹣2![]() ,
,
故答案为:4﹣2![]() .
.
(2)如图2中,
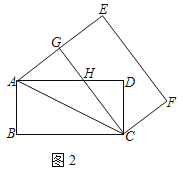
由四边形CGEF是矩形,得到∠CGE=90°,
∵点G在线段AE上,
∴∠AGC=90°,
∵CA=CA,CB=CG,
∴Rt△ACG≌Rt△ACB(HL).
∴∠ACB=∠ACG,
∵AB∥CD
∴∠ACG=∠DAC,
∴∠ACH=∠HAC,
∴AH=CH,设AH=CH=m,则DH=AD﹣AH=5﹣m,
在Rt△DHC中,∵CH2=DC2+DH2,
∴m2=22+(4﹣m)2,
∴m=![]() ,
,
∴AH=![]() ,GH=
,GH=![]() =
=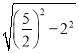 =
=![]() .
.
(3)在Rt△ABC中,![]() ,
,![]() ,
,
由题可知,G点在以C点为圆心,BC为半径的圆上运动,且GE与该圆相切,因为GE=AB不变,所以O到直线GE的距离即为△OGE的高,当点G在对角线AC上时,OG最短,即△OGE的面积最小,最小值=![]() ×OG×EG=
×OG×EG=![]() ×2×(4﹣
×2×(4﹣![]() )=4﹣
)=4﹣![]() .
.
当点G在AC的延长线上时,OG最长,即△OE′G′的面积最大.最大值=![]() ×E′G′×OG′=
×E′G′×OG′=![]() ×2×(4+
×2×(4+![]() )=4+
)=4+![]() .
.
综上所述,4﹣![]() ≤S≤4+
≤S≤4+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
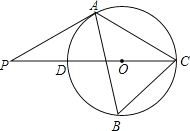
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+3的图象与坐标轴相交于点A(﹣2,0)和点B,与反比例函数y=![]() (x>0)相交于点C(2,m).
(x>0)相交于点C(2,m).
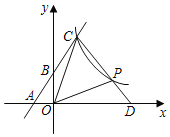
(1)填空:k1= ,k2= ;
(2)若点P是反比例函数图象上的一点,连接CP并延长,交x轴正半轴于点D,若PD:CP=1:2时,求△COP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
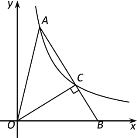
【题目】如图,在平面直角坐标系中,O为原点,点A在第一象限,点B是x轴正半轴上一点,∠OAB![]() 45°,双曲线
45°,双曲线![]() 过点A,交AB于点C,连接OC,若OC⊥AB,则tan∠ABO的值是_____.
过点A,交AB于点C,连接OC,若OC⊥AB,则tan∠ABO的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
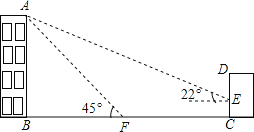
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函![]() ,下列说法中不正确的是( )
,下列说法中不正确的是( )
A.点![]() 在它的图象上
在它的图象上
B.它的图象在第一、三象限
C.当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
D.如果点![]() 在它的图象上,则点
在它的图象上,则点![]() 不在它的图象上
不在它的图象上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.

(1)判断AB与CD的关系并证明;
(2)求直线EC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com