
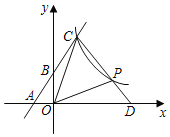
【题目】如图,一次函数y=k1x+3的图象与坐标轴相交于点A(﹣2,0)和点B,与反比例函数y=![]() (x>0)相交于点C(2,m).
(x>0)相交于点C(2,m).
(1)填空:k1= ,k2= ;
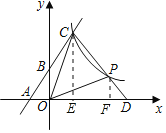
(2)若点P是反比例函数图象上的一点,连接CP并延长,交x轴正半轴于点D,若PD:CP=1:2时,求△COP的面积.
【答案】(1)![]() ,12;(2)S△COP=16.
,12;(2)S△COP=16.
【解析】
(1)先根据点A求出k1,再根据一次函数解析式求出m值,利用待定系数法求反比例函数的解析式;
(2)先根据三角形相似求得P点的坐标,然后利用三角形的面积差求解.S△COP=S△COD-S△POD.
(1)∵一次函数y=k1x+3的图象与坐标轴相交于点A(﹣2,0),
∴﹣2k1+3=0,
解得k1=![]() ,
,
∴一次函数为:y1=![]() x+3,
x+3,
∵一次函数y1=![]() x+3的图象经过点C(2,m).
x+3的图象经过点C(2,m).
∴m=![]() ×2+3=6,
×2+3=6,
∴C点坐标为(2,6),
∵反比例函数y=![]() (x>0)经过点C,
(x>0)经过点C,
∴k2=2×6=12,
故答案为![]() ,12.
,12.
(2)作CE⊥OD于E,PF⊥OD于F,
∴CE∥PF,
∴△PFD∽△CED,
∴![]() =
=![]() ,
,
∵PD:CP=1:2,C点坐标为(2,6),
∴PD:CD=1:3,CE=6,
∴![]() =
=![]() ,
,
∴PF=2,
∴P点的纵坐标为2,
把y=2代入y2=![]() 求得x=6,
求得x=6,
∴P(6,2),
设直线CD的解析式为y=ax+b,
把C(2,6),P(6,2)代入得![]() ,
,
解得![]() ,
,
∴直线CD的解析式为y=﹣x+8,
令y=0,则x=8,
∴D(8,0),
∴OD=14,
∴S△COP=S△COD﹣S△POD=![]() ×8×6﹣
×8×6﹣![]() =16.
=16.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】双曲线![]() (k为常数,且
(k为常数,且![]() )与直线
)与直线![]() 交于
交于![]() 两点.
两点.
(1)求k与b的值;
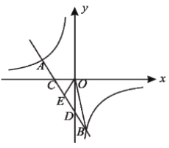
(2)如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受疫情影响,某种蔬菜的价格快速上涨,是原价的1.5倍,同样用48元能买到的蔬菜比原来少了2千克.
(1)求这种蔬菜的原价是每千克多少元?
(2)政府采取增加采购渠道、财政补贴等多种措施,降低特价,方便老百姓的生活.这种蔬菜的批改价两次下调后,由每千克10元降为每千克6.4元.求平均每次下调的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且HG=![]() BC,S△ABC =12,则图中阴影部分的面积为( )
BC,S△ABC =12,则图中阴影部分的面积为( )
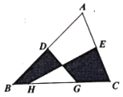
A.6B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
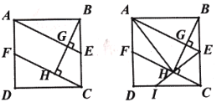
【题目】如图1,正方形ABCD中,点E是BC的中点,过点B作BG⊥AE于点G,过点C作CF垂直BG的延长线于点H,交AD于点F
(1)求证:△ABG≌△BCH;
(2)如图2,连接AH,连接EH并延长交CD于点I;
求证:① AB2=AE·BH;② 求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
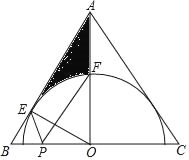
【题目】如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)求证:AC是⊙O的切线;
(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;
(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上任意一点(不与
上任意一点(不与![]() 重合)连接
重合)连接![]() ,过点M作
,过点M作![]() 交
交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() ,连接
,连接![]() .
.
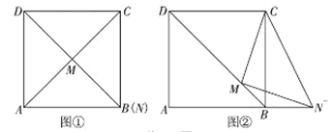
感知:如图①,当M为![]() 中点时,容易证
中点时,容易证![]() (不用证明);
(不用证明);
探究:如图②,点M为对角线![]() 上任意一点(不与
上任意一点(不与![]() 重合)请探究
重合)请探究![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
应用:(1)直接写出![]() 的面积S的取值范围;
的面积S的取值范围;
(2)若![]() ,则
,则![]() 与
与![]() 的数量关系是_____________.
的数量关系是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间某外地旅行团来重庆的网红景点打卡,游览结束后旅行社对该旅行团做了一次“我最喜爱的巴渝景点”问卷调查(每名游客都填了调査表,且只选了一个景点),統计后发现洪崖洞、长江索道、李子坝轻轨站、磁器口榜上有名.其中选李子坝轻轨站的人数比选磁器口的少![]() 人;选洪崖洞的人数不仅比选磁器口的多,且为整数倍;选磁器口与洪崖洞的人数之和是选李子坝轻轨站与长江索道的人数之和的
人;选洪崖洞的人数不仅比选磁器口的多,且为整数倍;选磁器口与洪崖洞的人数之和是选李子坝轻轨站与长江索道的人数之和的![]() 倍;选长江索道与洪崖洞的人数之和比选李子坝轻轨站与磁器口的人数之和多24人.则该旅行团共有_______人.
倍;选长江索道与洪崖洞的人数之和比选李子坝轻轨站与磁器口的人数之和多24人.则该旅行团共有_______人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com