
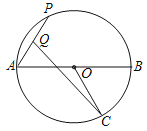
【题目】如图,AB是⊙O的直径,C为圆上一点,且∠AOC=120°,⊙O的半径为2,P为圆上一动点,Q为AP的中点,则CQ的长的最值是_____.
科目:初中数学 来源: 题型:
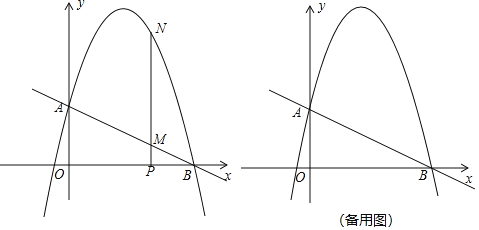
【题目】如图,已知直线y=﹣![]() x+2与x轴,y轴交于B,A两点,抛物线y=﹣x2+bx+c经过点A,B.
x+2与x轴,y轴交于B,A两点,抛物线y=﹣x2+bx+c经过点A,B.
(1)求这个抛物线的解析式;
(2)点P为线段OB上一个动点,过点P作垂直于x轴的直线交抛物线于点N,交直线AB于点M.
①点C是直线AB上方抛物线上一点,当△MNC∽△BPM相似时,求出点C的坐标.
②若∠NAB=60°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
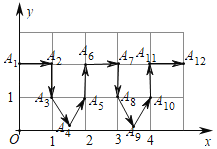
【题目】如图,点P在平面直角坐标系中按图中箭头所示的方向运动,每次运动一个单位,△A3A4A5和△A8A9A10都是等边三角形.第一次从(0,1)运动到点A1(0,2),第二次接着运动到点A2(1,2),第三次运动到点A3(1,1),…,经过2019次运动,动点P所在位置A2019的坐标是( )
A.(807,![]() )B.(
)B.(![]() ,2﹣
,2﹣![]() )
)
C.(![]() ,
,![]() )D.(807,2﹣
)D.(807,2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
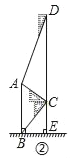
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73).
=1.73).

查看答案和解析>>
科目:初中数学 来源: 题型:
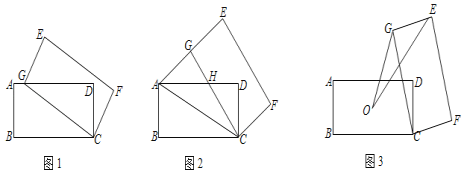
【题目】矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).
(1)如图1,当点G落在AD边上时,直接写出AG的长为 ;
(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;
(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工材料经销公司购进一种化工材料若干千克,价格为每千克40元,物价部门规定其销售单价不高于每千克70元,不低于每千克40元.经市场调查发现,日销量y(千克)是销售单价x(元)的一次函数,且当x=70时,y=80;x=60时,y=100.在销售过程中,每天还要支付其他费用350元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
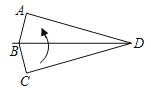
【题目】定义:有一组对角互补的四边形叫做互补四边形,如图,在互补四边形纸片ABCD中,BA=BC,AD=CD,∠A=∠C=90°,∠ADC=30°.将纸片先沿直线BD对折,再将对折后的纸片从一个顶点出发的直线裁剪,把剪开的纸片打开后铺平,若铺平后的纸片中有一个面积为4的平行四边形,则CD的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以一个等腰直角三角形的腰为边分别向形外做等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”.如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com