
【题目】以一个等腰直角三角形的腰为边分别向形外做等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”.如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .
科目:初中数学 来源: 题型:
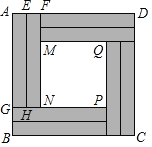
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是垂直于水平面的一棵树,小马(身高1.70米)从点A出发,先沿水平方向向左走2米到达P点处,在P处测得大树的顶端M的仰角为37°,再沿水平方向向左走8米到B点,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C点,然后再沿水平方向向左行走5米到达N点(A、B、C、N在同一平面内),则大树MN的高度约为( )(参考数据:tan37°≈0.75,sin37°≈0.60)
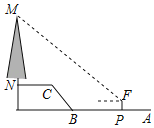
A.7.8米B.9.7米C.12米D.13.7米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州苏宁电器某品牌洗衣机销售情况良好,2018年11月份初该洗衣机每台的进价为2280元,购进了600台该品牌洗衣机.
(1)如果该商场为了减小库存压力,想把购进的600台该品牌洗衣机在11月底全部销售完,商场决定利用打折来促销,每台洗衣机在标价的基础上打8折,这样很快销售一空.要使该商场获得利润不低于72000元,则每台洗衣机的标价应不低于多少元?
(2)该商场决定12月初继续购进600台该品牌洗衣机销售,据悉,2018年12月份因全国经济出现通货膨胀,商品价格进一步上涨,商场决定该品牌洗衣机的销售价格比(1)中的最低标价上涨m%,但实际销售量比11月份下降了![]() m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.

(1)判断AB与CD的关系并证明;
(2)求直线EC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
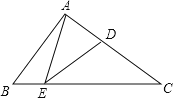
【题目】如图,在Rt△ABC中,已知∠BAC=90°,AB=6,AC=8,点D是AC上的一点,将△ABC沿着过点D的一条直线翻折,使点C落在BC边上的点E处,连接AE、DE,当∠CDE=∠AEB时,AE的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销甲、乙两种商品,已知一件甲种商品和一件乙种商品的进价之和为30元,每件甲种商品的利润是4元,每件乙种商品的售价比其进价的2倍少11元,小明在该商店购买8件甲种商品和6件乙种商品一共用了262元.
(1)求甲、乙两种商品的进价分别是多少元;
(2)在(1)的前提下,经销商统计发现,平均每天可售出甲种商品400件和乙种商品300件,如果将甲种商品的售价每提高0.1元,则每天将少售出7件甲种商品;如果将乙种商品的售价每提高0.1元,则每天将少售出8件乙种商品,经销商决定把两商品的价格都提高a元,在不考虑其他因素的条件下,当a为多少时,才能使该经销商每天销售甲、乙两种商品获取的利润共2500元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,1),B(1,0),PQ是直线y=x上的一条动线段且PQ=![]() (Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.
(Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com