
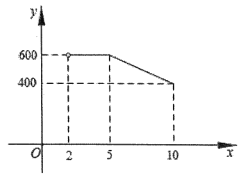
【题目】网络销售是一种重要的销售方式.某农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量![]() 与销售单价
与销售单价![]() (元)满足如图所示的函数关系(其中
(元)满足如图所示的函数关系(其中![]() ).
).
(1)若![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售单价![]() 为多少元时,每天的销售利润最大?最大利润是多少元?
为多少元时,每天的销售利润最大?最大利润是多少元?
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握我市中考模拟数学考试卷的命题质量与难度系数,调研老师在我市某地选取一个水平相当的初三年级进行调研,将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
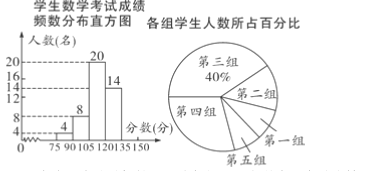
(1)本次调查共随机抽取了该年级___________名学生,考试成绩120分以上(含120分)学生有_________名;
(2)规定:成绩位于前5%的可获得小礼品一份,在被调查的学生中,某位学生成绩为134分,试判断他是否能获奖,说明理由;
(3)如果第一组![]() 中只有一名是女生,第五组
中只有一名是女生,第五组![]() 中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想…,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想…,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断:①当CD⊥AB时,EF为△ABC的中位线;②当四边形CEDF为矩形时,AC=BC;③当点D为AB的中点时,△CEF与△ABC相似;④当△CEF与△ABC相似时,点D为AB的中点.其中正确的是_____(把所有正确的结论的序号都填在横线上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=x2+bx+c
(1)若抛物线过点(2,﹣3),(4,5),求b、c.
(2)若抛物线过(﹣1,m2﹣m),(2,m2+2m),且﹣5≤m≤﹣3,求在m的变化过程中,抛物线最低点的坐标.
(3)直线y=2x+n与抛物线y=x2+bx+c交于A(﹣5,yA),B(﹣3,yB),把y=x2+bx+c向右平移t个单位(t>0)后交直线y=2x+n于C、D两点,若CD=2AB,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com