
【题目】为了掌握我市中考模拟数学考试卷的命题质量与难度系数,调研老师在我市某地选取一个水平相当的初三年级进行调研,将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
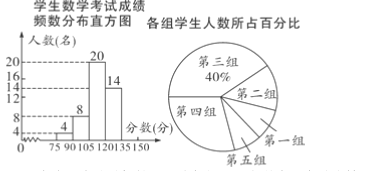
(1)本次调查共随机抽取了该年级___________名学生,考试成绩120分以上(含120分)学生有_________名;
(2)规定:成绩位于前5%的可获得小礼品一份,在被调查的学生中,某位学生成绩为134分,试判断他是否能获奖,说明理由;
(3)如果第一组![]() 中只有一名是女生,第五组
中只有一名是女生,第五组![]() 中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想…,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想…,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
【答案】(1)50,18;(2)不能;(3)见详解的树状图,![]()
【解析】
(1)用第三组的频数除以它的频率即可得到调查的总人数,然后计算出第五组的频数,再求出符合要求的频数和;
(2)先求出135分以上学生站的分数,再比较,看134分是否在其范围内;
(3)画树状图展示所有16种等可能的结果数,再找出所选两名学生刚好是一名女生和一名男生的结果数,然后根据概率公式求解.
解:(1)![]() ,
,
所以本次调查共随机抽取了该年级50名学生,
第五组的学生数为![]() ,
,
考试成绩120分以上(含120分)学生有:14+4=18
频数分布直方图补充为:
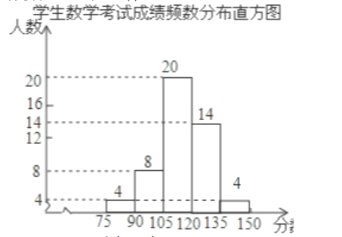
(2)不能获奖,理由是:
∵(135,150)这组人数占![]() 8%,8%>5%
8%,8%>5%
∴获奖成绩应在135分以上
∴成绩为134分的学生不能获奖
(3)画树状图为:

由树状图可知,共有16种等可能的结果数,其中所选两名学生刚好是一名女生和一名男生的结果数为10,
所以所选两名学生刚好是一名女生和一名男生的概率![]()


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() =
=![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
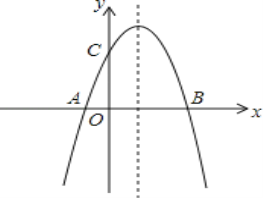
(1)求抛物线的解析式及顶点![]() 坐标;
坐标;
(2)在抛物线的对称轴上找到点![]() ,使得
,使得![]() 的周长最小,并求出点
的周长最小,并求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,若点![]() 是线段
是线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).过点
重合).过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .设
.设![]() 的长为
的长为![]() ,问当
,问当![]() 取何值时,
取何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场经销龟苓膏粉,其中![]() 品牌的批发价是每包20元,
品牌的批发价是每包20元,![]() 品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
(1)若购买这些龟苓膏粉共花费22000元,求两种品牌的龟苓膏粉各购买了多少包?
(2)若凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元,
若购买会员卡并用此卡购买这些龟苓膏粉共花费![]() 元,设
元,设![]() 品牌购买了
品牌购买了![]() 包,请求出
包,请求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 是由抛物线
是由抛物线![]() :
:![]() 平移得到的,并且
平移得到的,并且![]() 的顶点为(1,-4)
的顶点为(1,-4)
(1)求![]() 的值;
的值;
(2)如图1,抛物线C1与x轴正半轴交于点A,直线![]() 经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.
①若AP=AQ,求点P的坐标;
②若PA=PQ,求点P的横坐标.
(3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为16,设M、N两点的横坐标分别为m、n,求m与n的数量关系.
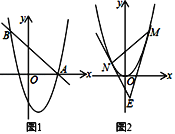
查看答案和解析>>
科目:初中数学 来源: 题型:
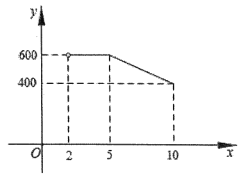
【题目】网络销售是一种重要的销售方式.某农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量![]() 与销售单价
与销售单价![]() (元)满足如图所示的函数关系(其中
(元)满足如图所示的函数关系(其中![]() ).
).
(1)若![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售单价![]() 为多少元时,每天的销售利润最大?最大利润是多少元?
为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依次类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形![]() 中,若
中,若![]() ,则平行四边形
,则平行四边形![]() 为1阶准菱形.
为1阶准菱形.
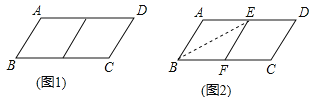
(1)判断与推理:
① 邻边长分别为2和3的平行四边形是__________阶准菱形;
② 小明为了剪去一个菱形,进行如下操作:如图2,把平行四边形![]() 沿着
沿着![]() 折叠(点
折叠(点![]() 在
在![]() 上)使点
上)使点![]() 落在
落在![]() 边上的点
边上的点![]() ,得到四边形
,得到四边形![]() ,请证明四边形
,请证明四边形![]() 是菱形.
是菱形.
(2)操作、探究与计算:
① 已知平行四边形![]() 的邻边分别为1,
的邻边分别为1,![]() 裁剪线的示意图,并在图形下方写出
裁剪线的示意图,并在图形下方写出![]() 的值;
的值;
② 已知平行四边形![]() 的邻边长分别为
的邻边长分别为![]() ,满足
,满足![]() ,请写出平行四边形
,请写出平行四边形![]() 是几阶准菱形.
是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC边的中点,以D为顶点作一个120°的角,角的两边分别交直线AB,AC于M,N两点,以点D为中心旋转∠MDN(∠MDN的度数不变),若DM与AB垂直时(如图①所示),易证BM +CN =BD.
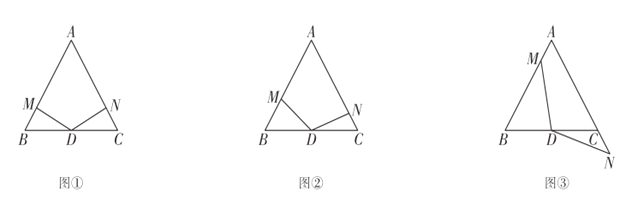
(1)如图②,若DM与AB不垂直时,点M在边AB上,点N在边AC上,上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图③,若DM与AB不垂直时,点M在边AB.上,点N在边AC的延长线上,上述结论是否成立?若不成立,请写出BM,CN,BD之间的数量关系,不用证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com