
����Ŀ��ij�����г��������߸�ۣ�����![]() Ʒ�Ƶ���������ÿ��20Ԫ��
Ʒ�Ƶ���������ÿ��20Ԫ��![]() Ʒ�Ƶ���������ÿ��25Ԫ��С���ƻ�����������Ʒ�ƵĹ��߸�۹�1000��������������⣺
Ʒ�Ƶ���������ÿ��25Ԫ��С���ƻ�����������Ʒ�ƵĹ��߸�۹�1000��������������⣺
��1����������Щ���߸�۹�����22000Ԫ��������Ʒ�ƵĹ��߸�۸������˶��ٰ���
��2����ƾ��Ա���ڴ������г�������Ʒ���Ի��8���Żݣ���Ա������Ϊ500Ԫ��
�������Ա�����ô˿�������Щ���߸�۹�����![]() Ԫ����
Ԫ����![]() Ʒ�ƹ�����
Ʒ�ƹ�����![]() ���������
���������![]() ��
��![]() ֮��ĺ�����ϵʽ.
֮��ĺ�����ϵʽ.
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
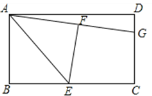
����Ŀ����ͼ���ھ���ABCD�У�E��BC�ߵ��е㣬����ABE��AE���ڵ�ֱ���۵��õ���AFE���ӳ�AF��CD�ڵ�G����֪CG=2��DG=1����BC�ij��ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ�
�ֱ�![]() �ᣬ
�ᣬ![]() ����A��B���㣬��CΪOB���е㣬��D�ڵڶ����ޣ����ı���AOCDΪ���Σ�
����A��B���㣬��CΪOB���е㣬��D�ڵڶ����ޣ����ı���AOCDΪ���Σ�

��1��ֱ��д����A��B�����꣬����ֱ��AB��CD����E�����ꣻ
��2������P�ӵ�C���������߶�CD��ÿ��1����λ���ȵ��ٶ����յ�D�˶���ͬʱ������N�ӵ�A���������߶�AO��ÿ��1����λ���ȵ��ٶ����յ�O�˶�������P��![]() ������ΪH������NP�����P���˶�ʱ��Ϊ
������ΪH������NP�����P���˶�ʱ��Ϊ![]() �룮
�룮
������NPH�����Ϊ1����![]() ��ֵ��
��ֵ��
����Q�ǵ�B���ڵ�A�ĶԳƵ㣬��![]() �Ƿ�����Сֵ������У������Ӧ�ĵ�P�����ꣻ���û�У���˵�����ɣ�
�Ƿ�����Сֵ������У������Ӧ�ĵ�P�����ꣻ���û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ� ABC �ı߳��� 2 �� D �� E �ֱ�Ϊ AB �� AC ���е㣬����CD ���� E ���� EF // DC �� BC ���ӳ����ڵ� F
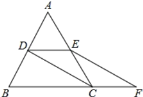
(1) ��֤:�ı��� CDEF ��ƽ���ı���;
(2)���ı��� CDEF ���ܳ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����
(1)��ͼ�٣��ڵ���ֱ��������ABC�У���ACB=90����CMƽ�֡�ACB��AB�ڵ�M����DΪ����CM��һ�㣬�Ե�CΪ��ת���Ľ��߶�CD��ʱ����ת90��õ��߶�CE������DE������CB�ڵ�F������BD��BE
��գ�
���߶�BD��BE��������ϵΪ______��
���߶�BC��DE��λ�ù�ϵΪ______��
�ƹ㣺
(2)��ͼ�ڣ��ڵ���������ABC�У����ǡ�ACB=a����CMƽ�֡�ACB��AB�ڵ�M����DΪ��ABC�ⲿ����CM��һ�㣬�Ե�CΪ��ת���Ľ��߶�CD��ʱ����ת���ȵõ��߶�CE������DE��BD��BE���ж�(1)�еĽ����Ƿ��������˵�����ɣ�
Ӧ�ã�
(3)��ͼ�ۣ��ڵȱ�������ABC�У�AB=4����BMƽ�֡�ABC��AC�ڵ�M����DΪ����BM��һ�㣬�Ե�BΪ��ת���Ľ��߶�BD��ʱ����ת60��õ��߶�BE������DE������BA�ڵ�F������AD��AE������A��D��MΪ��������������AEFȫ��ʱ����ֱ��д��DE��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ӭ��2022�걱�����»ᣬƼ�������ѧУ��֯��һ�δ��ͳ��ܱ������ף��������ڱ���ʱ��·��![]() (��)��ʱ��
(��)��ʱ��![]() (����)�Ĺ�ϵ��ͼ��ʾ������ͼ������������:
(����)�Ĺ�ϵ��ͼ��ʾ������ͼ������������:

(1)��γ��ܱ�����ȫ����___�ף��ȵ����յ���˱���һ��������____����:
(2)����ѧУ�ᄊ���˶�Ա��ʮ��ע��������ɣ��������̷����ܡ�;���ܳ�������Σ����������μ��ٹ���.�ʵ�![]() ����ʱ�һ���������?
����ʱ�һ���������?
(3)�������ڵ�һ�μ��ٺ�ʼ�ձ�������ٶȼ���ǰ������ô�ף�������˭�ȵ����յ�?��˵������.
(4)��ʵ�����ϼ�ʱ���Ƕ��ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��

��1����֤����CBG�ա�CDG��
��2������HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У��ı���AEBD�ܷ�Ϊ���Σ�����ܣ��������H�����ꣻ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������
��ͼ��BEƽ����ABD��DEƽ����BDC�������������£�90�㣬��˵����AB��CD.

����������̣�
��BEƽ�֡�ABD(��֪)��
���ABD��2����(__________)��
��DEƽ�֡�BDC(��֪)��
���BDC��2���� (__________)��
���ABD����BDC��2������2������2(����������)( __________)��
�ߡ�����������90��(��֪)��
���ABD����BDC��180��(__________)��
��AB��CD(____________________)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪һ�κ���y����![]() x+6��x��y��ֱ���A��B���㣬��C��0��n�����߶�BO��һ�㣬����AOB��ֱ��AC�۵�����B�պ�����x�Ḻ�����ϣ����C�������ǣ�������
x+6��x��y��ֱ���A��B���㣬��C��0��n�����߶�BO��һ�㣬����AOB��ֱ��AC�۵�����B�պ�����x�Ḻ�����ϣ����C�������ǣ�������

A. ��0��3�� B. ��0��![]() �� C. ��0��
�� C. ��0��![]() �� D. ��0��
�� D. ��0��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com