
 如图,点C在⊙O的直径BA的延长线上,AB=2AC,CD切⊙O于点D,连接CD,OD.
如图,点C在⊙O的直径BA的延长线上,AB=2AC,CD切⊙O于点D,连接CD,OD.分析 (1)根据CD切⊙O于点D,得出CD⊥OD,再根据AB=2CA,求出∠C=30°,即可得出答案;
(2)连接AD,证得△DAO是等边三角形,求出DA=r=2,再根据勾股定理可求得BD的长.
解答 解:(1)∵CD切⊙O于点D,
∴CD⊥OD,
又∵AB=2AC,
∴OD=AO=AC=$\frac{1}{2}$CO
∴∠C=30°
∴tan∠C=$\frac{\sqrt{3}}{3}$;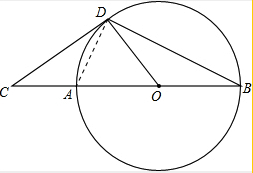 (2)连接AD,
(2)连接AD,
∵AB是直径,
∴∠ADB=90°,
∵∠DOA=90°-30°=60°,
又∵OD=OA,
∴△DAO是等边三角形.
∴DA=r=2,
∴DB=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 此题考查了切线的性质,用到的知识点是切线的性质、三角函数的定义、勾股定理,关键是根据题意作出辅助线,得出直角三角形.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x=5 | B. | x=-7 | C. | x=-13 | D. | x=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 出生年份 | 2022年年龄(岁) | 延迟退休时间(年) | 实际退休年龄(岁) |
| 1967 | 55 | 0.5 | 55.5 |
| 1968 | 54 | 1 | 56 |
| 1969 | 53 | 1.5 | 56.5 |
| 1970 | 52 | 2 | 57 |
| 1971 | 51 | 2.5 | 57.5 |
| 1972 | 50 | 3 | 58 |
| … | … | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com