
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
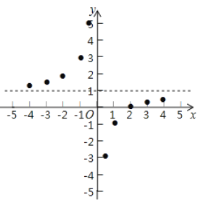
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)如图所示,见解析;(2)①增大;②上,1;③![]() ;(3)1.
;(3)1.
【解析】
(1)按要求把![]() 轴左边点和右边各点分别用一条光滑曲线顺次连接起来即可;
轴左边点和右边各点分别用一条光滑曲线顺次连接起来即可;
(2)①观察图像可得出函数增减性;②由表格数据及图像可得出平移方式;③由图像可知对称中心;
(3)将![]() 与
与![]() 联立求解,得到A、B两点坐标,将△AOB分为△AOC与△BOC计算面积即可.
联立求解,得到A、B两点坐标,将△AOB分为△AOC与△BOC计算面积即可.
(1)如图所示:
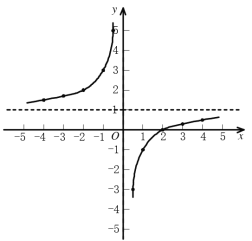
(2)①由图像可知:当![]() 时,
时,![]() 随
随![]() 的增大而增大,故答案为:增大;
的增大而增大,故答案为:增大;
②由表格数据及图像可知,![]() 的图象是由
的图象是由![]() 的图象向上平移1个单位而得到的,故答案为:上,1;
的图象向上平移1个单位而得到的,故答案为:上,1;
③由图像可知图像关于点(0,1)中心对称.
(3)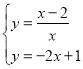 ,解得:
,解得:![]() 或
或![]()
∴A点坐标为(-1,3),B点坐标为(1,-1)
设直线![]() 与y轴交于点C,当x=0时,y=1,
与y轴交于点C,当x=0时,y=1,
所以C点坐标为(0,1),如图所示,
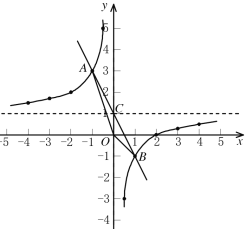
S△AOB= S△AOC+ S△BOC
=![]()
=![]()
=![]()
所以△AOB的面积为1.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() 过点
过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() .设
.设![]()

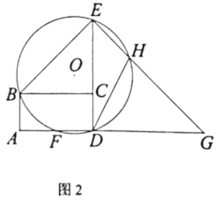
(1)连结![]() ,请求出
,请求出![]() 的度数和
的度数和![]() 的半径(用
的半径(用![]() 的代数式表示). (直接写出答案)
的代数式表示). (直接写出答案)
(2)证明:点![]() 是
是![]() 的中点.
的中点.
(3)如图2,延长![]() 至点
至点![]() ,使得
,使得![]() , 连结
, 连结![]() ,交
,交![]() 于点
于点![]()
①连结![]() ,当
,当![]() 与四边形
与四边形![]() 其它三边中的一边相等时,请求出所有满足条件的
其它三边中的一边相等时,请求出所有满足条件的![]() 的值.
的值.
②当点![]() 关于直线
关于直线![]() 对称点
对称点![]() 恰好落在
恰好落在![]() 上,连结
上,连结![]() .记
.记![]() 和
和![]() 的面积分别为
的面积分别为![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),经多次测试后,得到如下部分数据:
x/米 | 0 | 0.2 | 0.4 | 0.6 | 1 | 1.4 | 1.6 | 1.8 | … |
y/米 | 0.24 | 0.33 | 0.4 | 0.45 | 0.49 | 0.45 | 0.4 | 0.33 | … |
(1)由表中的数据及函数学习经验,求出y关于x的函数解析式;
(2)试求出当乒乓球落在桌面时,其落点与端点A的水平距离是多少米?
(3)当乒乓球落在桌面上弹起后,y与x之间满足![]() .
.
①用含a的代数式表示k;
②已知球网高度为0.14米,球桌长(1.4×2)米.若a=-0.5,那么乒乓球弹起后,是否有机会在某个击球点可以将球沿直线扣杀到端点A?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
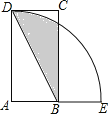
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
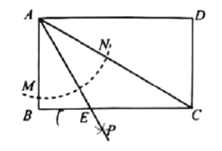
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=-2x+mx+n经过点A(0,2),B(3,-4).
(1)求该抛物线的函数表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点),如果直线CD与图象G有两个公共点,结合函数的图象,求点D纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
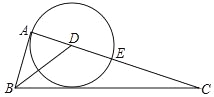
【题目】如图,在Rt△ABC中,∠BAC=90°,BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E
(1)求证:BC是⊙D的切线;
(2)若AB=5,BC=13,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
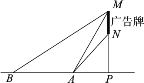
【题目】我校数学社团成员想利用所学的知识测量某广告牌的宽度(图中线段MN的长).直线MN垂直于地面,垂足为点P,在地面A处测得点M的仰角为60°,点N的仰角为45°,在B处测得点M的仰角为30°,AB=5米.且A、B、P三点在一直线上,请根据以上数据求广告牌的宽MN的长.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com